13.2 模型基本形式

假设有\(M\)个数据集，\(p\)个解释变量。第\(m\)个数据集的样本量为\(n^{(m)}\)，因变量\(y^{(m)}\)为\(n^{(m)} \times 1\)向量，解释变量\(X^{(m)}\)为\(n^{m} \times p\)矩阵，假设数据已经被标准化。

对第\(m\)个数据集建立如下模型：

\[ y^{(m)}=X^{(m)}\beta^{(m)}+\epsilon^{(m)} \tag{13.1} \]

其中，\(\beta^{(m)}=(\beta_1^{(m)}, \cdots,\beta_p^{(m)})'\)为回归系数，\(\epsilon^{(m)}\)满足\(E(\epsilon^{(m)})=0\)、\(Var(\epsilon^{(m)})=\sigma^2_{(m)}\)。

由此拓展到所有数据集中，则

\[ \beta=\textrm{argmin}\{L(X,y;\beta)+P(\beta;\lambda)\} \tag{13.2} \]

其中\(y=(y^{(1)'},\cdots,y^{(M)'})'\)为\(\sum\limits_{m=1}^M n^{(m)} \times 1\)的因变量，\(X=diag(X^{(1)},\cdots,X^{(m)})\)为\(\sum\limits_{m=1}^M n^{(m)} \times Mp\)的设计矩阵，\(\beta=(\beta^{(1)'},\cdots,\beta^{(M)'})'\)为\(Mp \times 1\)的未知参数向量。\(L(X,y;\beta)=\sum\limits_{i=1}^M L(X^{(m)},y^{(m)};\beta^{(m)})\)是所有数据集上的损失之和，\(L(\cdot)\)可取平方损失或负向对数似然损失。\(P(\lambda;\beta)\)是惩罚函数，\(\lambda\)用于调控惩罚力度，\(\lambda\)越大，惩罚力度越大，\(\beta\)被压缩得越严重，估计为零的回归系数也就越多。

\[ \begin{pmatrix} y^{(1)}\\ \vdots \\ y^{(m)} \end{pmatrix}= \begin{pmatrix} X^{(1)}\beta^{(1)}+\epsilon^{(1)}\\ \vdots \\ X^{(m)}\beta^{(m)}+\epsilon^{(m)} \end{pmatrix}= \begin{pmatrix} X^{(1)} & & \\ & \ddots & \\ & & X^{(m)} \end{pmatrix} \begin{pmatrix} \beta^{(1)} \\ \vdots \\ \beta^{(m)} \end{pmatrix}+ \begin{pmatrix} \epsilon^{(1)} \\ \vdots \\ \epsilon^{(m)} \end{pmatrix} \]

记\(X_j\)在所有数据集中的回归系数为\(\beta_j=(\beta_j^{(1)},\cdots,\beta_j^{(m)})'\)。在整合分析中，由于\(\beta_j\)归属于同一个自变量\(X_j\)，故\(\beta_j\)内部之间具有一定程度的关联性或相似性，即可将其视为群组。

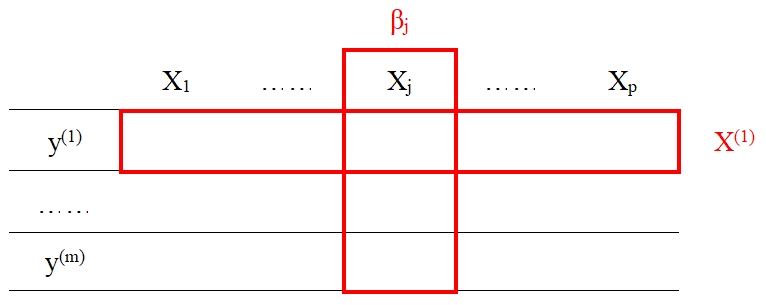
图 13.1: 数据结构