16.3 群组变量选择
本节是对《高维数据下群组变量选择的惩罚方法综述》[18]的讨论。
解释变量的分组结构可以分为两类:自然分组和人为分组。
自然分组由先验信息划分,例如描述分类变量的虚拟变量组(季节、学历等)。
人为分组则是在某种目的下将高度相关的变量归为一组,例如在公司财务评价中会把销售毛利率、净资产收益率、总资产报酬率等指标归为“盈利能力”。常见的分组依据为相关系数。
无论是自然分组还是人为分组,都是解释变量的集合,即群组变量,由此引申出群组变量选择方法。
在群组变量情形下,将自变量分为\(J\)个组别,即\(X=(X_1,\cdots,X_J)\)依旧是\(n \times p\)维设计矩阵,对应的系数向量为\(\beta=(\beta^{(1)'},\dots,\beta^{(J)'})'\),其中\(X_j=(x_{j1},\cdots,x_{jp_j})\),\(\beta^{(j)}=(\beta_1^{(j)},\cdots,\beta_{p_j}^{(j)})\)。目标函数形式同式(16.4)。
16.3.2 处理高度相关数据的组变量选择方法
在处理高度相关数据时,惩罚函数是具有单个变量选择功能的函数和处理高度相关数据的函数的线性组合,其一般形式为
\[ P_{\lambda_1,\lambda_2}(| \beta |)=\sum_{j=1}^pf_{\lambda_1}(| \beta_j |)+\lambda_2|| \beta ||_2^2 \tag{16.14} \]
不难发现,式(16.14)的惩罚函数具有共同的组成部分,即\(L_2\)正则项\(|| \beta ||_2^2\)。文献[19]指出,如果\(X'X\)不是近似单位阵的话,那么最小二乘估计将会变得异常敏感。而为\(X'X\)加上\(kI\)则能有效控制系数估计值的膨胀及不稳定性。
为什么共线性会导致系数膨胀?
根据文献[19],记\(L_1^2=(\hat{\beta}-\beta)'(\hat{\beta}-\beta)\),可得\(E(L_1^2)=\sigma^2\sum\limits_{i=1}^p (1/\lambda_i)\),\(Var(L_1^2)=2\sigma^4\sum\limits_{i=1}^p (1/\lambda_i)^2\)。当共线性严重时,会导致\(X'X\)的最小特征值十分接近0,从而导致较大的\(E(L_1^2)\)和\(Var(L_1^2)\),即系数估计值膨胀及不稳定。
岭回归的解为
\[ \hat{\beta}_{ridge}=(X'X+\lambda I)^{-1}X'Y \tag{16.15} \]
岭回归通过引入可控的偏差从而有效地减少了系数估计的方差。
也就是增大了\(X'X\)特征值
优点
- 通过引入L2正则化项,可以解决特征数量多于样本数量时的过拟合问题。
- 能够处理特征间高度相关的情况。
缺点
- 虽然可以缩小系数,但不会将系数压缩到零,因此不会进行特征选择。
- 需要选择合适的正则化参数。
16.3.2.1 Enet
glmnet包的glmnet()函数
\(Enet\)首先见刊于Hui Zou & Trevor Hastie[20]的文章。
Hui Zou也是\(Adaptive \; Lasso\)的创造者。
\(Enet\)的惩罚函数为
\[ P_{\lambda}(| \beta |)=\lambda_1\sum_{j=1}^p| \beta_j |+\lambda_2\sum_{j=1}^p \beta_j^2 \tag{16.16} \]
首先观察\(\frac{1}{2}| \beta |+\frac{1}{2}\beta^2\)的图像,图片摘自原文。
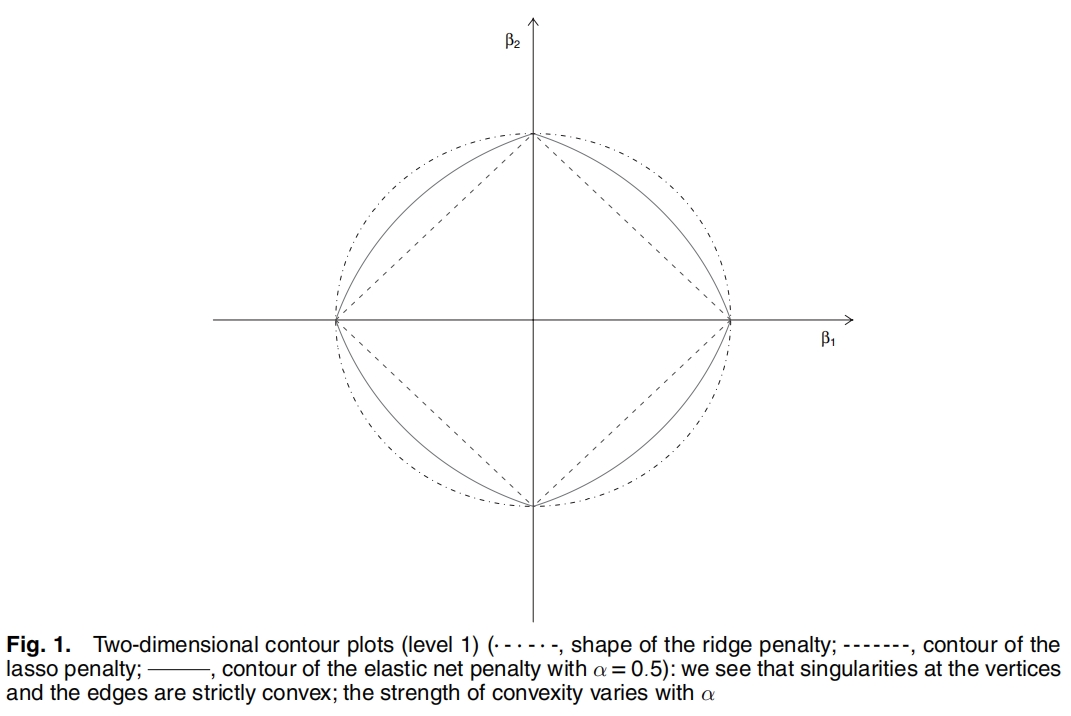
图 16.11: Enet惩罚函数
\(\alpha=\frac{\lambda_2}{\lambda_1+\lambda_2}\)
正如注解中说的,\(Enet\)惩罚函数在顶点处是奇异的,在边处是凸的,并且这种凸性与\(\alpha\)挂钩。
原文同样也给出了\(OLS\)、\(Lasso\)、\(Ridge\)、\(naive \;elastic \; net\)的解,如下图所示。
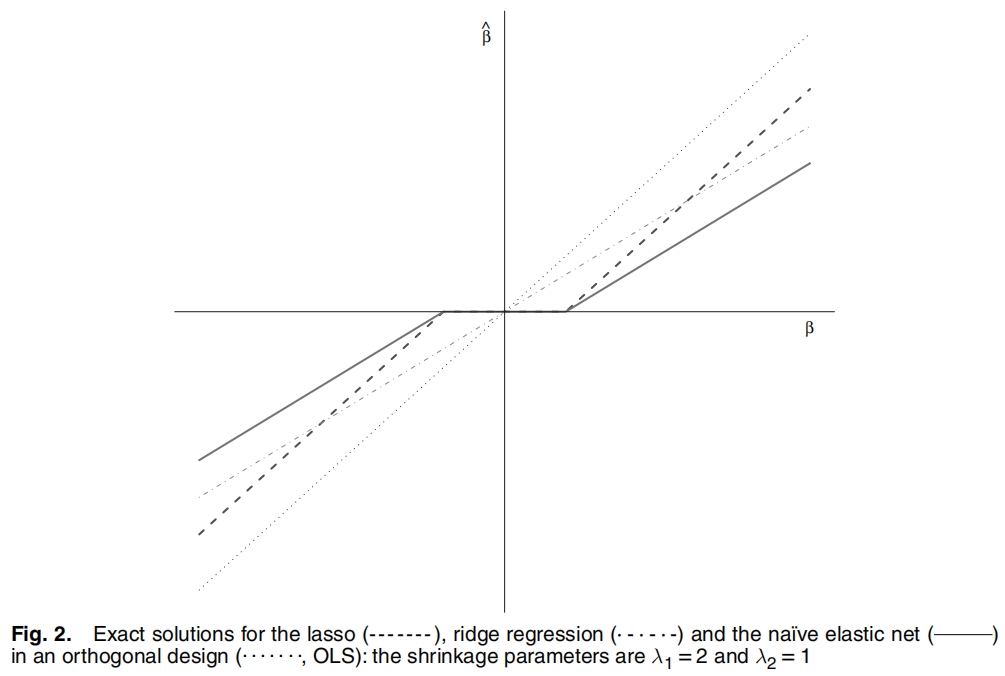
图 16.12: 弹性网的解
\(Enet\)的解在一开始与\(Lasso\)的解保持一致,均为0,但在达到阈值之后就同\(Ridge\)一样逐渐增大惩罚力度。
the naive elastic net can be viewed as a two-stage procedure: a ridge-type direct shrinkage followed by a lasso-type thresholding.
这里提到的
naive elastic net的解是对原数据进行数据变换后的解,在数据变换后可以作为\(Lasso\)回归处理。后文又提到了elastic net的解,该解是在前者的基础上乘上\((1+\lambda_2)\),使得该解在保留前者优良性质的基础上还能取消对系数的压缩。
\(Enet\)解的具体表达式如下所示
为了后面引用方便,这个解的表达式摘自\(Mnet\)的文献[21]
\[ \begin{aligned} \hat{\theta}_{nEnet} &= sgn(z)\frac{(| z |-\lambda_1)}{1+\lambda_2} \\ \tilde{\theta}_{Enet} &= (1+\lambda_2)\hat{\theta}_{nEnet} \end{aligned} \tag{16.17} \]
原文也提到了对分组效应的看法:“定性地说,如果一组高度相关的变量的回归系数趋于相等(如果是负相关的,则达到符号的变化),那么回归方法就会表现出分组效应。特别是,在某些变量完全相同的极端情况下,回归方法应该给相同的变量分配相同的系数”。
并且,原文通过\(Lemma \; 2\)表明严格凸惩罚函数(例如\(L_2\)正则项)在极端情况(变量间高度相关)下能够识别出分组效应,并且同组变量的回归系数估计值将会趋同,反观\(L_1\)正则项甚至没有唯一解。\(Theorem \; 1\)则给出了两个高度相关的变量的差异上界,这种差异在相关系数为1下几乎为0。由于\(Enet\)中包含了\(L_2\)正则项,因此能够处理高度相关的变量,即具有群组变量选择的功能。
原文提到\(Lasso\)的三个缺点,前两个详见\(Least Angle Regression\)原文[22],第三个详见\(Lasso\)原文[15]。
优点
- 综合了岭回归和\(Lasso\)的优点,既能很好地处理高度相关的数据,又能选择变量。
- 当\(p>>n\)时,在不可表条件以及其他一些复杂条件下,弹性网具有\(Oracle\)性质。
缺点
- 往往选择过多的变量组。
- 一般情形下不具有\(Oracle\)性质。
16.3.2.2 Mnet
ncvreg包的ncvreg()函数
Jian Huang等人[23]提出的\(Mnet\)法结合了\(MCP\)函数[21]和\(L_2\)正则项。
\(Mnet\)的惩罚函数为
\[ P_{\lambda , a}(| \beta |)=\sum_{j=1}^p f_{\lambda_1,a}^{MCP}(| \beta_j |)+\frac{1}{2}\lambda_2\sum_{j=1}^p \beta_j^2 \tag{16.18} \]
其中
\[ f_{\lambda,a}^{MCP}(\theta)= \begin{cases} \lambda\theta-\frac{\theta^2}{2a}, & \theta \leq a \lambda \\ \frac{a\lambda^2}{2}, & \theta \gt a \lambda \end{cases} \tag{16.19} \]
\[ f_{\lambda,a}^{'MCP}(\theta)= \begin{cases} \lambda-\frac{\theta}{a}, & \theta \leq a \lambda \\ 0, & \theta \gt a \lambda \end{cases} \tag{16.20} \]
原文中提到\(MCP\)惩罚函数会使得结果是无偏的,稀疏的和连续的。
式(16.18)和式(16.16)相比,将\(L_1\)正则项换为MCP函数。
\(f_{\lambda_1,a}^{MCP}(| \beta |)+\frac{\lambda_2}{2}\beta^2\)的函数图像如图16.13所示。
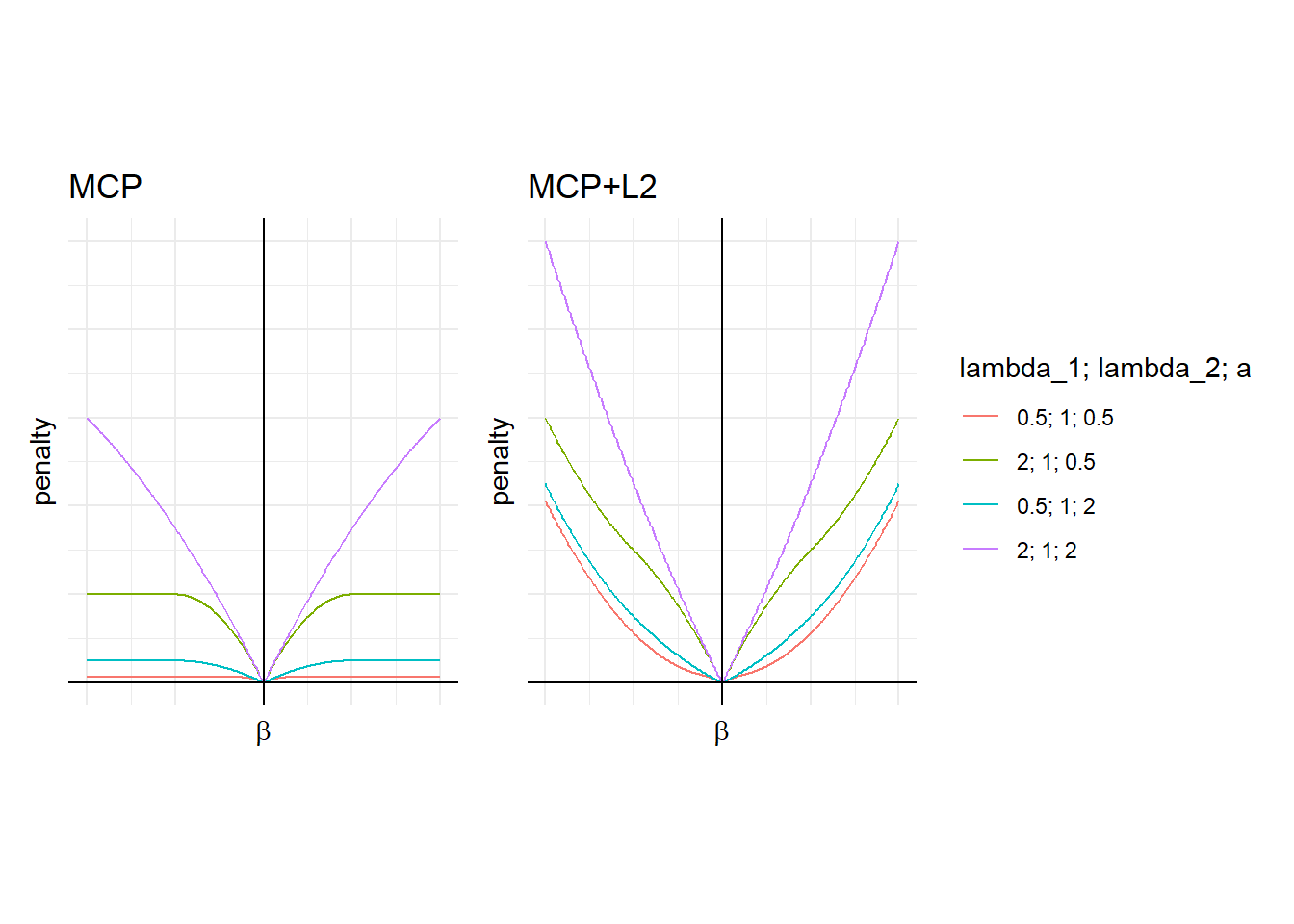
图 16.13: Mnet的惩罚函数
原文还给出了\(Mnet\)的解与\(Enet\)的解之间的联系,结合式(16.17),有
\[ \begin{aligned} \hat{\theta}_{Mnet}&= \begin{cases} sgn(z)\frac{a(| z |-\lambda_1)_{+}}{a(1+\lambda_2)-1}, & | z | \leq a \lambda_1(1+\lambda_2) \\ \frac{z}{1+\lambda_2}, & | z | \gt a \lambda_1(1+\lambda_2) \end{cases} \\ \tilde{\theta}_{sMnet}&= \begin{cases} \frac{a(1+\lambda_2)}{a(1+\lambda_2)-1}\hat{\theta}_{Enet}, & | z | \leq a \lambda_1(1+\lambda_2) \\ z, & | z | \gt a \lambda_1(1+\lambda_2) \end{cases} \end{aligned} \tag{16.21} \]
\(Mnet\)的解通过尺度变化(和\(Enet\)一样都是乘上\(1+\lambda_2\)),不仅能取消对估计值的压缩,还能得到无偏估计。
而在分组效应方面,和\(Enet\)一样,\(Mnet\)原文也给出了两个高度相关的变量之间差异的上界,这意味高度相关的自变量能够被\(Mnet\)识别出来。
优点
- 在处理高度相关问题时比弹性网更具优势。
- 在\(p>n\)或\(p<n\)时,在某些合理条件下,\(Mnet\)能正确选择具有非零系数的解释变量且用岭回归来估计相应的参数,因此具有\(Oracle\)性质。
16.3.2.3 SCAD_l2
ncvreg包的ncvreg()函数
Zeng和Xie[24]提出的\(SCAD\_l_2\)法综合了\(SCAD\)函数和\(L_2\)正则项。
《高维数据下群组变量选择的惩罚方法综述》引用的Group variable selection for data with dependent structures[25]并没有\(SCAD\_L_2\),而是介绍\(gLars\)和\(gRidge\)算法。
\(SCAD\_l_2\)的惩罚函数为
\[ P_{\lambda, a}(| \beta |)=\sum_{j=1}^p f_{\lambda_1,a}^{SCAD}(\beta_j)+\lambda_2\sum_{j=1}^p \beta_j^2 \tag{16.22} \]
其中
\[ f_{\lambda,a}^{SCAD}(\theta)= \begin{cases} \lambda | \theta |, & 0 \leq | \theta | \lt \lambda \\ -\frac{\theta^2-2a\lambda| \theta |+\lambda^2}{2(a-1)}, &\lambda \leq | \theta | \lt a\lambda \\ \frac{(a+1)\lambda^2}{2}, &a\lambda \leq | \theta | \end{cases} \tag{16.23} \]
原文中给出了\(SCAD\_L_2\)的解和惩罚函数,分别如图16.14、图16.15所示。
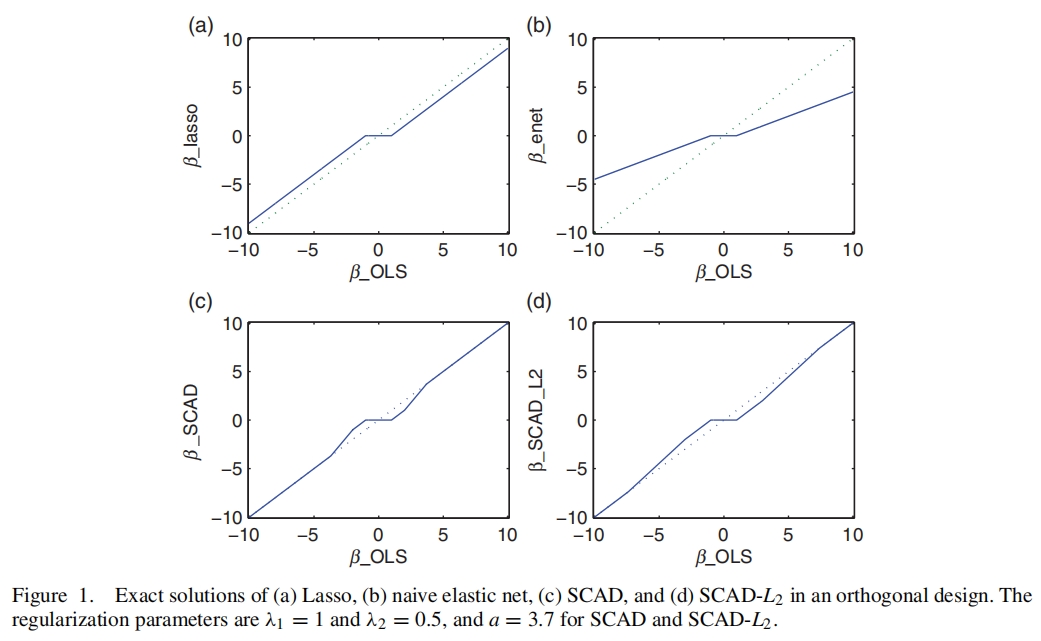
图 16.14: SCAD_L2的解
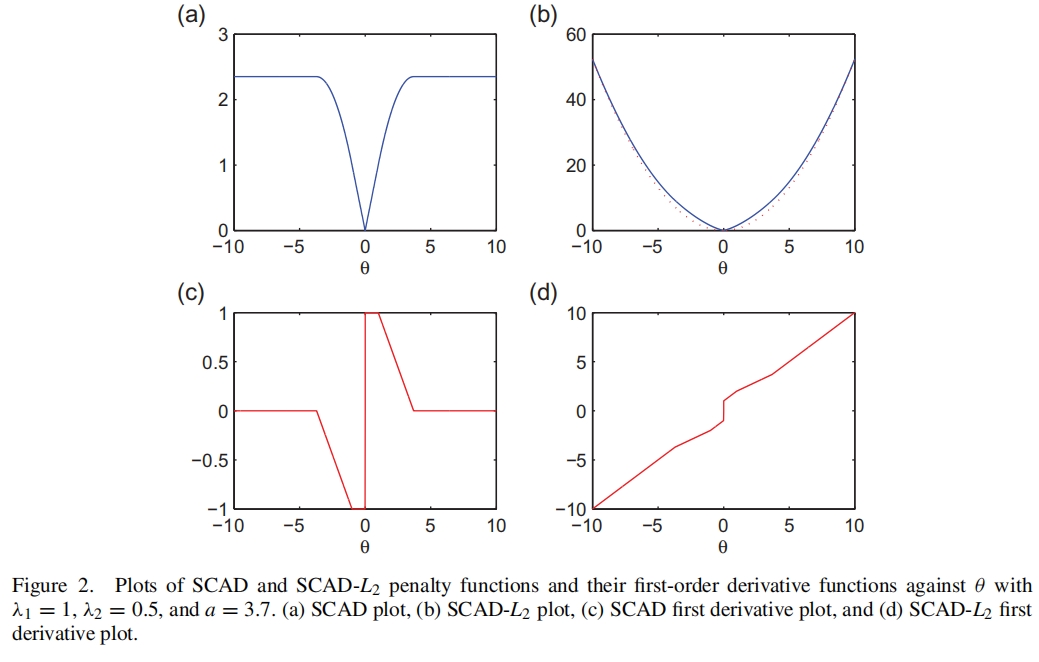
图 16.15: SCAD_L2的惩罚函数
解的具体表达式如下所示
\[ \hat{\theta}_{naive}= \begin{cases} \frac{sgn(z)(| z | -\lambda_1)_{+}}{1+2\lambda_2}, &| z | \leq 2\lambda_1(1+\lambda_2) \\ \frac{(a-1)z-a\lambda_1sgn(z)}{-1+(a-1)(1+2\lambda_2)}, &2\lambda_1(1+\lambda_2) \lt | z | \leq a\lambda_1(1+2\lambda_2) \\ \frac{z}{1+2\lambda_2}, & a\lambda_1(1+2\lambda_2) \lt | z | \end{cases} \tag{16.24} \]
当\(| z |\)较大时,\(\hat{\theta}_{SCAD\_L_2} = (1+2\lambda_2)\hat{\theta}_{naive}\)也是无偏的,与式(16.21)不谋而合。
而在分组效应方面,相同作者的另一篇文献[25]定义了“群组变量”的概念:(1)和因变量或者残差高度相关;(2)组内变量之间高度相关。和\(Enet\)的文献一样,原文证明了\(SCAD\_L_2\)的惩罚函数是严格凸的,并且同样也给出了差异上界,故该方法也具有识别群组变量的功能。
优点
- 在模拟分析中,与\(Lasso\)、\(SCAD\)和\(Enet\)相比,该方法不仅能降低预测误差、保留模型的稀疏性质,而且能揭露变量更多的分组信息。
- 估计值具有无偏性、连续性、稀疏性和群组效应。
16.3.2.4 小结
这三种方法都是依靠\(L_2\)正则项来实现群组变量的识别,加之另一惩罚函数来实现单个变量选择。
三者都是通过证明惩罚函数是严格凸的或者变量之间的差异上界随着相关程度增加而趋于0来表明自己的方法能够识别群组变量。
除了\(Enet\),\(Mnet\)和\(SCAD\_L_2\)在系数估计值较大时都具有无偏性。
这个性质是在设计矩阵为列正交阵的条件下证明的。正如文献[23]中提到的,对于一般情形,为了无偏性而做的尺度变换会增加估计的均方误差,又因为尺度变换不影响方法在筛选变量过程中呈现出来的性质,故一般不考虑尺度变换。
16.3.3 仅能选择组变量的方法
前一类方法将具有高度相关的数据视为同一个群组,但变量的组结构并不明确。下面介绍的方法则是在已知组结构的情形下对整租变量同时选择或者删除。这类方法的惩罚函数形如
\[ P_{\lambda}(| \beta |)=\lambda\sum_{j=1}^JP_{outer}(\sum_{k=1}^{p_j}P_{inner}(| \beta_k^{(j)}|)) \tag{16.25} \]
这类方法的组间惩罚函数具有单个变量选择功能,通过将组内对系数的惩罚和视作一个整体从而实现对组别的选择。而组内惩罚函数不具有单个变量选择功能,故该类方法只能选择重要组而不能选择组内的重要变量。
16.3.3.1 Group Lasso
gglasso包的gglasso()函数 orgrpreg包的grpreg函数
Yuan和Lin[26]在其文章中除了给出了\(Group \; Lasso\),还讨论了\(Group \; Lar\)、\(Group \; non-negative \; garrotte\),这里仅讨论\(Group \; Lasso\)。
\(Group \; Lasso\)的惩罚函数为
\[ P_{\lambda,K}(| \beta |)=\lambda \sum_{j=1}^J || \beta^{(j)} ||_{K_j} \tag{16.26} \]
其中\(||\beta^{(j)}||_{K_j}=(\beta^{(j)'}K_j\beta^{(j)})^{\frac{1}{2}}\)为由\(K_j\)决定的椭圆范数,\(K_j\)为\(p_j\)阶正定对称矩阵。椭圆范数有
\[ \begin{aligned} ||\beta^{(j)}||_{K_j}&=(\beta^{(j)'}K_j\beta^{(j)})^{\frac{1}{2}} \\ &= (\beta^{(j)'}Q\Lambda Q'\beta^{(j)})^{\frac{1}{2}} \\ &= [(\Lambda^{\frac{1}{2}}Q'\beta^{(j)})'(\Lambda^{\frac{1}{2}}Q'\beta^{(j)})]^{\frac{1}{2}} \end{aligned} \tag{16.27} \]
可见椭圆范数就是线性变换后的\(L_2\)范数。
原文给出了\(K_j\)的建议值,即\(K_j=p_jI_j\),故式(16.26)转化为
\[ P_{\lambda,K}(| \beta |)=\lambda \sum_{j=1}^J \sqrt{p_j}|| \beta^{(j)} ||_2 \tag{16.28} \]
式(16.28)的组内惩罚即为带权重的组内系数的\(L_2\)范数。不妨记组内惩罚为\(a_j=\sqrt{p_j}|| \beta^{(j)} ||_2\),当然有\(a_j \geq 0\)。回忆\(L_1\)范数的定义,\(||x||_1=\sum\limits_{i=1}^p |x_i|\),式(16.28)中的对应部分为\(\sum\limits_{j=1}^J a_j\),也就是说,若将组内惩罚值视作新的分量,那么组间惩罚的形式就是\(L_1\)范数。
原文对\(L_1\)、\(Group \; Lasso\)、\(L_2\)的惩罚函数进行了可视化,如图16.16所示。
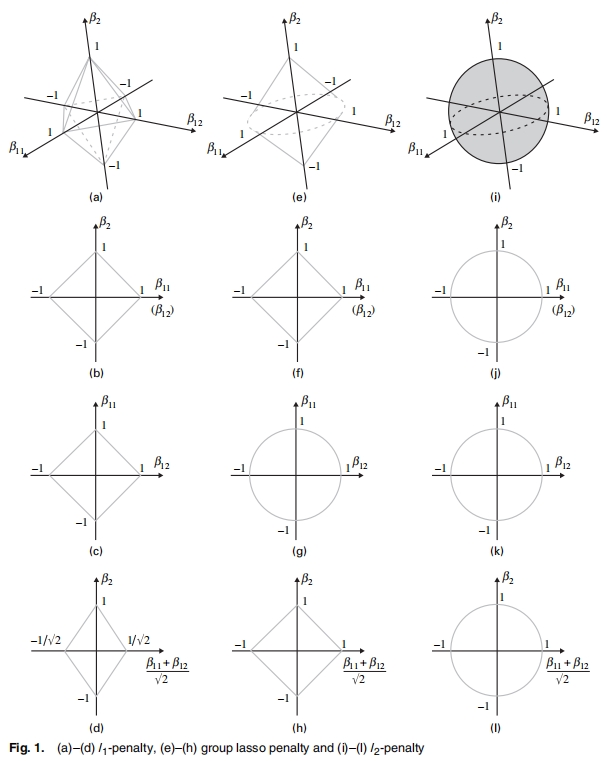
图 16.16: Group Lasso的惩罚函数
可以发现式(16.28)介于\(L_1\)正则项与\(L_2\)正则项之间。其中子图\((e)\)反映了\(||\beta_1||+|\beta2|=1\)。
优点
- 对于确定的\(p\),在不可表条件的变形条件下,\(Group \; Lasso\)在随机设计模型中具有组选择一致性。
缺点
- \(Group \; Lasso\)不具备\(Oracle\)性质。
- 参数估计值偏差过大,也往往会选择过多的组。
16.3.3.2 CAP
\(CAP\)也是在已知群组结构的情形下进行群组变量选择的方法。Zhao等人[27]提到了可以利用聚类技术先去进行分组,然后再进行群组变量选择。此外,原文还提到了重叠与非重叠群组的概念,而\(CAP\)对这两种情形均适用。
Specifically, we introduce the Composite Absolute Penalties (CAP) family, which allows given grouping and hierarchical relationships between the predictors to be expressed.
Grouped selection occurs for nonoverlapping groups. Hierarchical variable selection is reached by defining groups with particular overlapping patterns.
\(CAP\)惩罚函数的一般形式为
\[ P_{\lambda, \gamma}(|\beta|)=\lambda||(||\beta^{(1)}||_{\gamma_1},\cdots,||\beta^{(J)}||_{\gamma_J})'||_{\gamma_0}^{\gamma_0} \tag{16.29} \]
不难发现,组间惩罚函数为\(||\cdot||_{\gamma_0}^{\gamma_0}\),组内惩罚函数为\(||\cdot||_{\gamma_j}\)。相较于式(16.28),式(16.29)在组内惩罚函数的形式方面给予了更多的灵活度。这使得\(CAP\)不仅能处理非重叠群组,还能处理重叠群组。
非重叠群组就是指各个组分配到的变量没有重复,该情形较为容易理解,这里就不再赘述。
对于重叠群组,这里仅考虑有\(X_1\)、\(X_2\)的简单情形。若我们想让\(X_1\)在\(X_2\)之前选入模型,我们可以构造这样的群组关系,令\(G_1=\{X_1, X_2\}\)、\(G_2=\{X_2\}\)、\(\gamma_0=1\)、\(\gamma_1,\gamma_2>1\),对此有
\[ P_{\lambda,\gamma}(|\beta|)=\lambda(||(\beta_1,\beta_2)||_{\gamma_1}+||\beta_2||_{\gamma_2}) \tag{16.30} \]
其中\(||\beta_2||_{\gamma_2}=|\beta_2|\)。绘制\(||(\beta_1,\beta_2)||_{\gamma_1}+|\beta_2|\)的等值线图,如下所示:
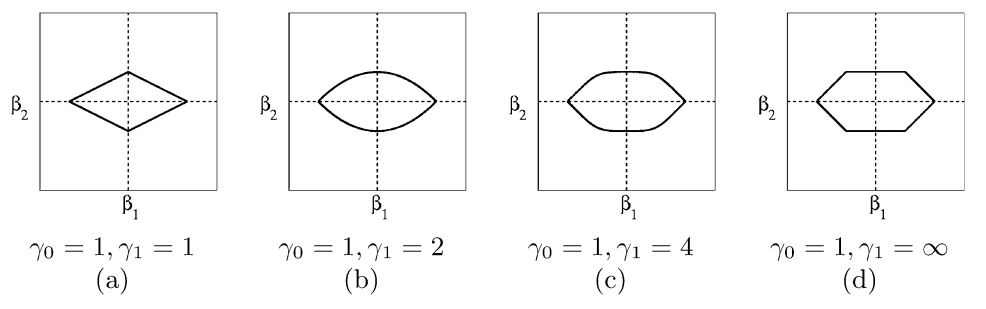
图 16.17: 重叠群组的惩罚函数
当\(\gamma_1 > 1\)时,\(\beta_1\)轴上尖尖的特征愈发明显,而\(\beta_2\)轴上愈发平坦。因此,\(\beta_1\)轴更容易与损失函数相交,此时\(\beta_2=0\)。可见,若想让一个变量先于另一个变量被选入到模型中,应当将这两个变量放在同一个组别中,并且另一个变量单独处于一个组。
优点
- 允许组组之间存在重叠变量。
16.3.4 双层变量选择方法
双层变量选择方法既能选择重要组别,又能在组内选择重要变量。
在这一节中,双层变量选择法又分为两类方法,第一类称为“复合函数惩罚法”,该类方法通过复合函数的形式来选择重要对象。因此组内惩罚函数与组间惩罚函数都应该是具有单个变量选择功能的惩罚函数。惩罚函数的形式同式(16.25)。第二类称为“稀疏组惩罚法”,该类方法凭借具有单个变量选择功能的惩罚函数和具有仅能选择组变量功能的惩罚函数的线性组合来选择对象,又称为“可加惩罚”,其一般形式为
\[ P_{\lambda_1,\lambda_2}(|\beta|)=\lambda_1P_{indiv}(|\beta|)+\lambda_2P_{grp}(|\beta|) \tag{16.31} \]
16.3.4.1 Group Bridge
grpreg包的grpreg函数
Huang等人[28]提出的\(Group \; Bridge\)属于“复合函数惩罚法”,其惩罚函数形式为
\[ P_\lambda(|\beta|)=\sum\limits_{j=1}^J\lambda c_j||\beta^{(j)}||_1^\gamma \tag{16.32} \]
其中\(0<\gamma<1\),\(c_j\)是一个调整参数,可取\(c_j \propto |A_j|^{1-\gamma}\),\(|A_j|\)表示第\(j\)组的变量数。注意组内系数的正则项为\(||\beta^{(j)}||_1^\gamma\),即先求得\(\beta^{(j)}\)的\(L_1\)范数,再求其\(\gamma\)次幂,组间求和的形式就是\(L_\gamma\)范数。结合图16.1可知,当\(0<\gamma<1\)时,\(L_\gamma\)范数在结点处是奇异的,故也能产生稀疏解。因此\(Group \; Bridge\)在组内和组间都能进行变量选择。
该方法的惩罚函数图像如图16.18所示。
文献[28]中提到\(Group \; Bridge\)也允许重叠群组的存在。
优点
- 当\(p \rightarrow \infty, \, n \rightarrow \infty\)但\(p<n\)时,在某些正则条件下,\(Group \; Bridge(0<\gamma<1)\)具有群组\(Oracle\)性质。
缺点
- 不具备组内相合性。
16.3.4.2 Group MCP
grpreg包的grpreg函数
\(Group \; Bridge\)的惩罚函数结合了\(L_1\)正则项与\(L_\gamma\)正则项(\(0<\gamma<1\)),因此在某些点是奇异的,即不可微。故Breheny和Huang[29]提出的\(Group \; MCP\)采用\(MCP\)函数来作为组间及组内惩罚函数。在\(MCP\)的原始文献[21]中已经证明了该惩罚函数具有无偏性、连续性和稀疏性。
\(Group \; MCP\)的惩罚函数为
\[ P_{\lambda, a, b}(|\beta|)=\sum\limits_{j=1}^Jf_{\lambda,b}^{MCP}(\sum\limits_{k=1}^{p_j}f_{\lambda, a}^{MCP}(|\beta_k^{(j)}|)) \tag{16.33} \]
由式(16.19)可知,当\(\beta>a\lambda\)时,\(f_{\lambda,a}^{MCP}(\beta)\)取得最大值\(\frac{a\lambda^2}{2}\)。当组内的各个系数均大于\(a\lambda\)时,组内惩罚达到最大值,即\(p_j\frac{a\lambda^2}{2}\)。之后将组内惩罚值传入到组间惩罚函数,此时需比较\(b\lambda\)与\(p_j\frac{a\lambda^2}{2}\)的大小,显然当\(p_j\frac{a\lambda}{2}>b\)时,组间惩罚也取到了最大值。
此外,与\(Group \; Lasso\)和\(Group \; Bridge\)相比,原文指出了\(Group MCP\)无论是在个体变量选择上还是组别选择上都是capped,如图16.18所示。
不知道怎么翻译
the group MCP penalty is capped at both the individual covariate and group levels, while the group lasso and group bridge penalties are not.
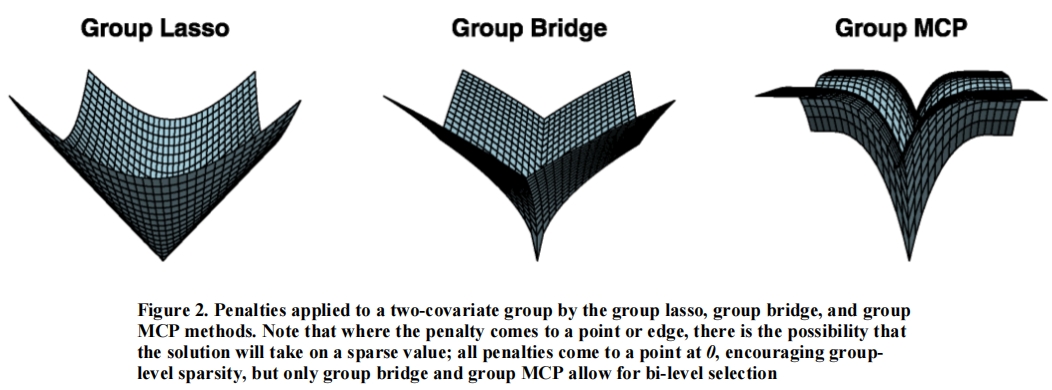
图 16.18: Group MCP的惩罚函数
该图表明\(Group \; MCP\)方法能够有效避免过度惩罚较大的系数,同时保持解的稀疏性。
之后,原文写了一段耐人寻味的文字。
Group bridge allows the presence of a single large predictor to continually lower the entry threshold of the other variables in its group. This property, whereby a single strong predictor drags others into the model, prevents group bridge from achieving consistency for the selection of individual variables. Group MCP, on the other hand, limits the amount of signal that a single predictor can contribute towards the reduction of the penalty applied to the other members of the group.
\(Group \; Bridge\)的惩罚函数对系数的惩罚是一直存在的,并且系数越大,惩罚越大。在群组变量的背景下,当一个系数真的很大时,该系数就会极大地增加该组的组内惩罚函数值,尽管其他系数对组内惩罚函数值的贡献十分有限。这样从外人(组间惩罚函数)的视角来看就会觉得这一组变量挺重要的,实则滥竽充数,颇有“一人得道,鸡犬升天”的意味。
而\(Group \; MCP\)的惩罚函数对系数的惩罚是有限的,这就确保了当组内较大的系数摆脱了非零的嫌疑后,他就可以撒手不管,组内惩罚函数值的大小还得靠其他系数来一起做贡献,“大家好才是真的好”。
与文献[18]的论断相反,有待商榷。
优点
- 具有组内和组间的相合性。
16.3.4.3 Sparse Group Lasso
sparsegl包的sparsegl()函数
Simon等人[30]提出的\(Sparse Group Lasso\)的惩罚函数如下所示
\[ P_\lambda(|\beta|)=\lambda_1||\beta||_1+\lambda_2\sum\limits_{j=1}^J ||\beta^{(j)}||_2 \tag{16.34} \]
不难发现,式(16.34)就是\(L_1\)正则项加上\(Group \; Lasso\)中除去\(\sqrt{p_j}\)的惩罚项,式(16.28)。该方法依靠\(L_1\)正则项进行单个变量选择,依靠\(Group \; Lasso\)的部分进行群组变量选择,从而实现既能选择单个重要变量,又能选择重要组别。当然,也正如文章中说的,第一项和第二项被具有相应功能的惩罚项替代也是可以的。