16.1 准备
16.1.1 范数
向量\(x=(x_1, \cdots,x_n)\)的\(L_p\)范数被定义为:
\[ || x ||_p=\sqrt[p]{\sum_i^{n} | x_i | ^p} \tag{16.1} \]
常见的有\(L_1\)范数与\(L_2\)范数(一般会以平方的形式出现),如下所示:
\[ || x ||_1 = \sum_i^n | x_i | \tag{16.2} \]
\[ || x ||_2^2 = \sum_i^n x_i^2 \tag{16.3} \]
以二元系数为例,\(L_p\)范数的示例如图16.1所示:
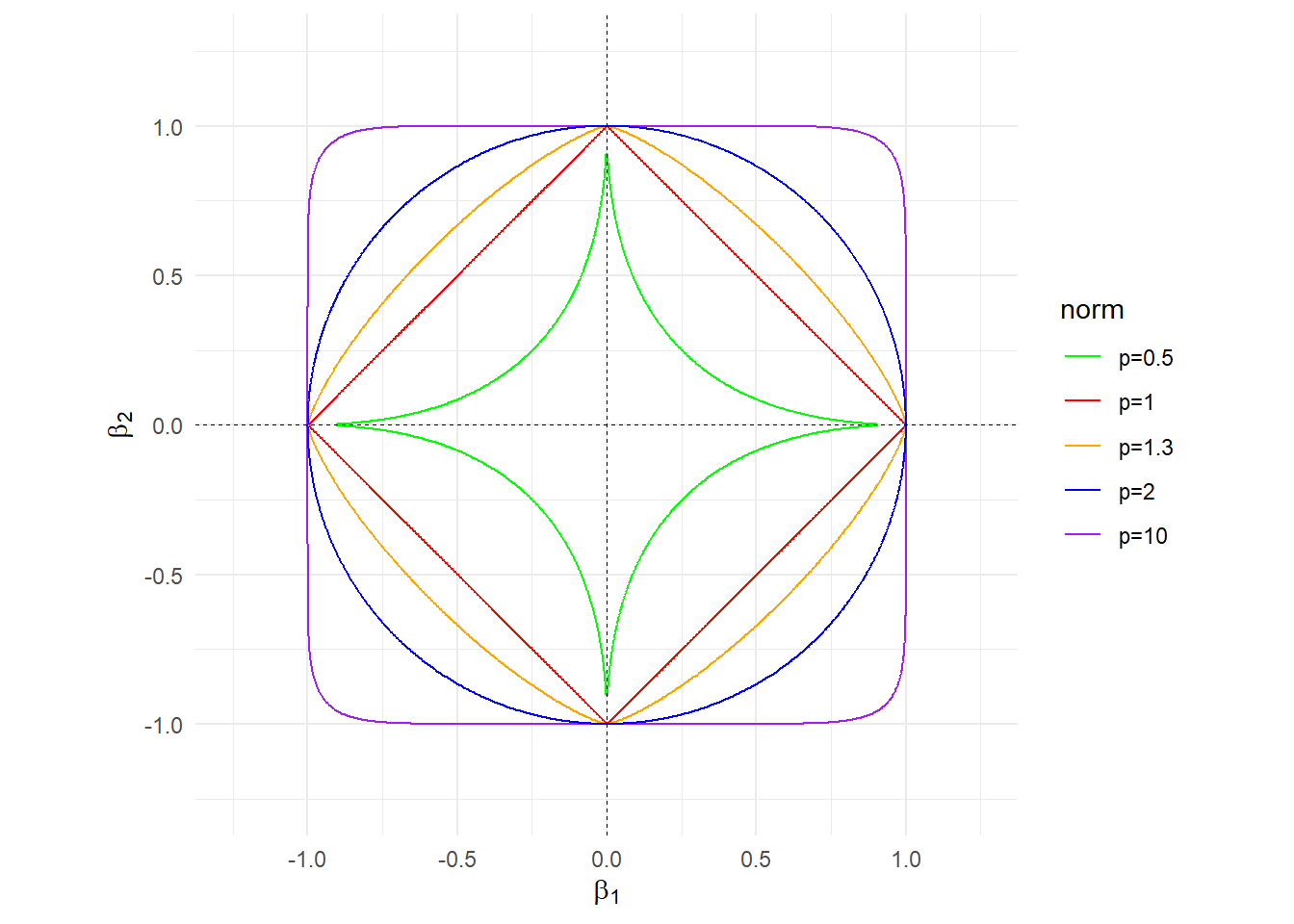
图 16.1: Lp范数示意图
16.1.2 目标函数
目标函数是我们的优化目标,其一般形式为:
\[ Q(\beta)=L(\beta | y,X)+P_{\lambda}(| \beta |) \tag{16.4} \]
其中\(y=(y_1,\cdots ,y_n)'\)是因变量,\(X=(x_1,\cdots,x_p)\)是\(n \times p\)维设计矩阵,\(\beta=(\beta_1,\dots,\beta_p)'\)为系数向量,\(L(\cdot)\)和\(P_\lambda(\cdot)\)分别表示具体的损失函数和惩罚函数。
可以看到,目标函数由两部分组成:损失函数\(L(\beta | y,X)\)与惩罚函数\(P_{\lambda}(| \beta |)\)。其示意图如图16.2所示。
图 16.2: 目标函数分解
下面分别对\(OLS\)、\(Lasso\)、\(Ridge\)进行数据模拟。
假设真实函数为
\[ y=3 \times x_1+ 0 \times x_2 \tag{16.5} \]
其中\(y\)仅与\(x_1\)有关。对此我们生成20组观测值,
# 生成数据
set.seed(111)
x1 <- runif(20)
x2 <- runif(20)
epsilon <- rnorm(20)
y <- 2*x1+epsilon
df <- tibble(y=y, x1=x1, x2=x2)然后计算\(OLS\)、\(Lasso\)、\(Ridge\)对应的估计值。
ols <- lm(y~0+x1+x2, df) # 0表示不加截距项
library(glmnet)
# glmnet是弹性网回归,alpha的值控制L1正则和L2正则之间的权重
# 当alpha=1即lasso回归;当alpha=2即ridge回归
lasso_cv <- cv.glmnet(x=as.matrix(df[,2:3]), y=df$y, family='gaussian', intercept=F, alpha=1, nfolds=5)
lasso <- glmnet(x=as.matrix(df[,2:3]), y=df$y, family='gaussian', intercept=F, alpha=1, lambda=lasso_cv$lambda.min)
ridge_cv <- cv.glmnet(x=as.matrix(df[,2:3]), y=df$y, family='gaussian', intercept=F, alpha=0, nfolds = 5)
ridge <- glmnet(x=as.matrix(df[,2:3]), y=df$y, family='gaussian', intercept=F, alpha=0, lambda=ridge_cv$lambda.min)
paste0('OLS_1:', round(ols$coefficients[1],3), ';OLS_2:', round(ols$coefficients[2],3))
paste0('Lasso_1:', round(coef(lasso)[2],3), ';Lasso_2:', round(coef(lasso)[3],3))
paste0('Ridge_1:', round(coef(ridge)[2],3), ';Ridge_2:', round(coef(ridge)[3],3))[1] "OLS_1:2.554;OLS_2:-0.742"
[1] "Lasso_1:1.405;Lasso_2:0"
[1] "Ridge_1:0.959;Ridge_2:0.22"接下来看看不同系数是怎样影响目标函数的取值。
# 目标函数
objective_fun <- function(beta1, beta2, df, type='ols', lambda){
xxx = df
response = as.matrix(xxx$y)
predictor = as.matrix(xxx[,2:3])
loss = sum((response - predictor %*% c(beta1, beta2))^2)/(2*nrow(df))
switch(type,
'ols' = {
penalty = 0
lambda = 0
},
'lasso' = {
penalty = abs(beta1) + abs(beta2)
},
'ridge' = {
penalty = (beta1^2 + beta2^2)/2
}
)
result = loss + lambda*penalty
result
}
# 网格采样,设置系数组合
grid_parameter <- expand.grid(seq(-3, 3, 0.05), seq(-3, 3, 0.05))
colnames(grid_parameter) <- c('beta1', 'beta2')
# 计算不同采样点对应的目标函数值
grid_parameter <- grid_parameter %>%
rowwise() %>%
mutate(OLS = objective_fun(beta1, beta2, df),
L1 = abs(beta1) + abs(beta2),
Lasso = objective_fun(beta1, beta2, df, type='lasso', lambda=lasso$lambda),
L2 = beta1^2 + beta2^2,
Ridge = objective_fun(beta1, beta2, df, type='ridge', lambda=ridge$lambda))
head(grid_parameter)# A tibble: 6 × 7
# Rowwise:
beta1 beta2 OLS L1 Lasso L2 Ridge
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 -3 -3 7.62 6 10.1 18 46.7
2 -2.95 -3 7.54 5.95 10.0 17.7 46.0
3 -2.9 -3 7.46 5.9 9.90 17.4 45.3
4 -2.85 -3 7.37 5.85 9.80 17.1 44.6
5 -2.8 -3 7.29 5.8 9.70 16.8 43.9
6 -2.75 -3 7.21 5.75 9.60 16.6 43.2
glmnet()函数[13]使用的目标函数为\(\frac{RSS}{2n}+\lambda \ast (\frac{(1-\alpha )}{2}|| \beta ||_2^2+\alpha || \beta ||_1)\),为保持损失函数一致,故将ols的损失函数乘上\(\frac{1}{2n}\),最小二乘解保持不变。
下面可视化不同回归的目标函数值变化情况。
图 16.3: OLS+Lasso
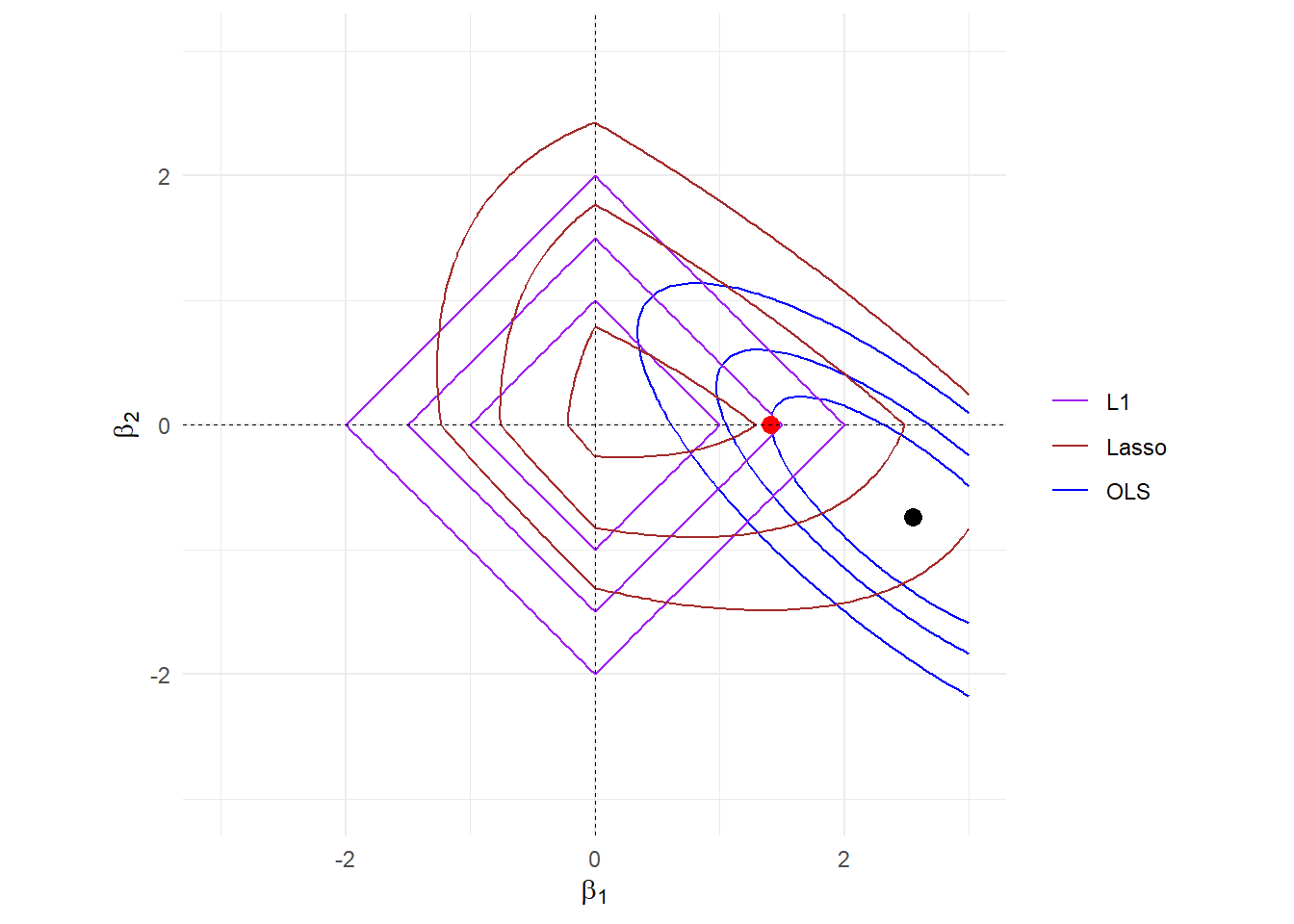
图 16.4: contour of OLS+Lasso
\(L_1\)正则项的存在使得目标函数有非常明显的沟槽。
图 16.5: OLS+Ridge
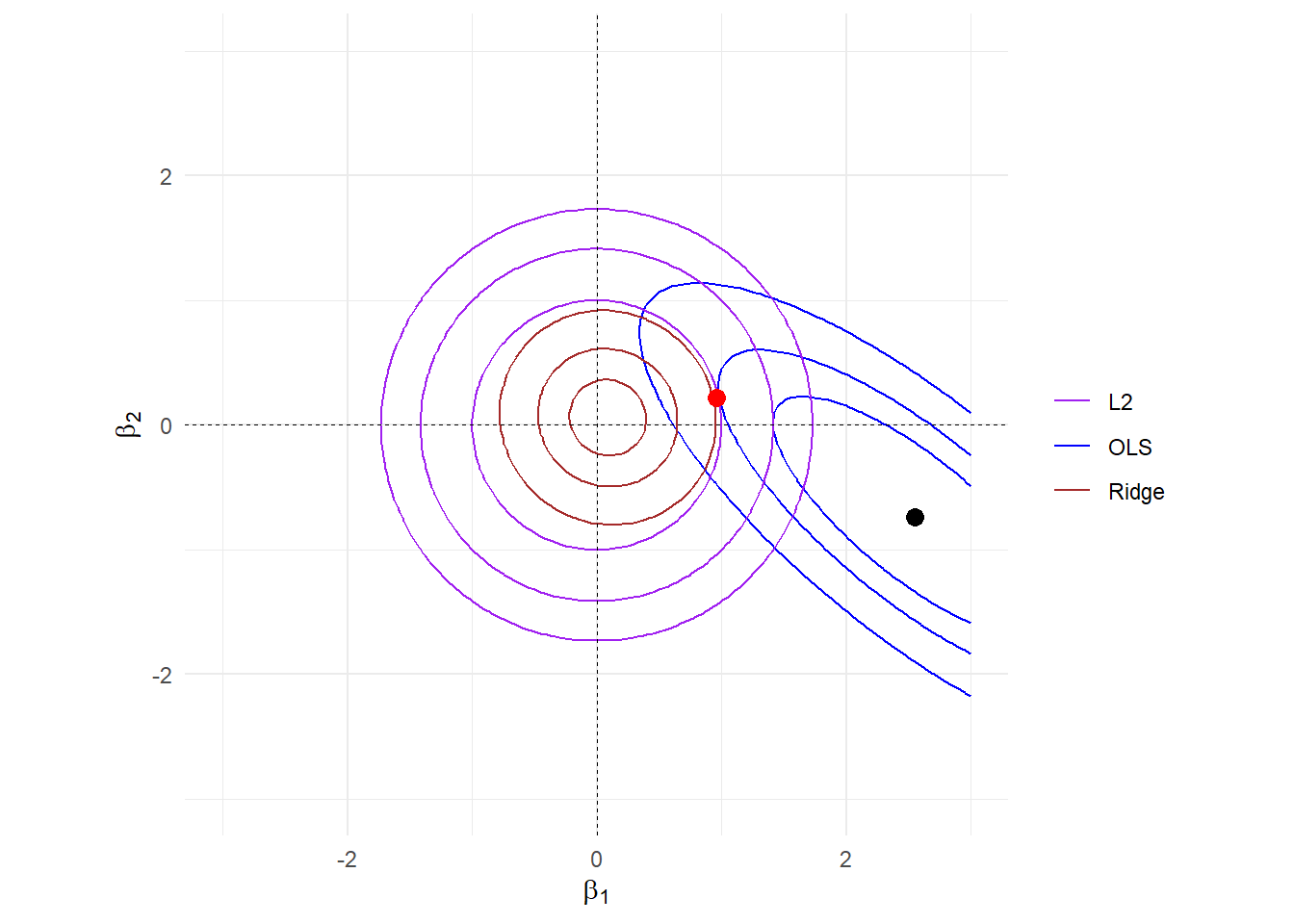
图 16.6: contour of OLS+Ridge
glmnet()函数在不同的\(\lambda\)下使用坐标下降算法[13]进行迭代,满足一定条件后就会停止迭代,因此得到的结果会与模拟数据的最小值点存在差异。
惩罚函数的存在使得系数向原点方向收缩,并改变了目标函数的形态,形态决定功能,由此产生目标解。
为什么损失函数是椭圆状?对于任意一个估计\(\tilde \beta\),有
\[ \begin{aligned} Q&=(Y-X\tilde{\beta})'(Y-X\tilde{\beta}) \\ &=(Y-\hat{Y}+\hat{Y}-X\tilde{\beta})'(Y-\hat{Y}+\hat{Y}-X\tilde{\beta}) \\ &=(e+X(\hat{\beta}-\tilde{\beta}))'(e+X(\hat{\beta}-\tilde{\beta})) \\ &=e'e+e'X(\hat{\beta}-\tilde{\beta})+(\hat{\beta}-\tilde{\beta})'X'e+(\hat{\beta}-\tilde{\beta})'X'X(\hat{\beta}-\tilde{\beta}) \\ &=e'e+(\hat{\beta}-\tilde{\beta})'X'X(\hat{\beta}-\tilde{\beta}) \end{aligned} \tag{16.6} \]
其中\(X'e=0\),\(\hat \beta\)是最小二乘估计。对于\((\hat{\beta}-\tilde{\beta})'X'X(\hat{\beta}-\tilde{\beta})\),有
\[ \begin{aligned} (\hat{\beta}-\tilde{\beta})'X'X(\hat{\beta}-\tilde{\beta})&=(\hat{\beta}-\tilde{\beta})'Q\Lambda Q'(\hat{\beta}-\tilde{\beta}) \\ &=(Q'(\hat{\beta}-\tilde{\beta}))'\Lambda(Q'(\hat{\beta}-\tilde{\beta})) \end{aligned} \tag{16.7} \]
可见\((Q'(\hat{\beta}-\tilde{\beta}))'\Lambda(Q'(\hat{\beta}-\tilde{\beta}))\)就是椭圆的表达式。