10.4 LSTM
10.4.1 原理
在学习LSTM之前,可以先了解一下RNN,再去看LSTM。
【LSTM长短期记忆网络】3D模型一目了然,带你领略算法背后的逻辑
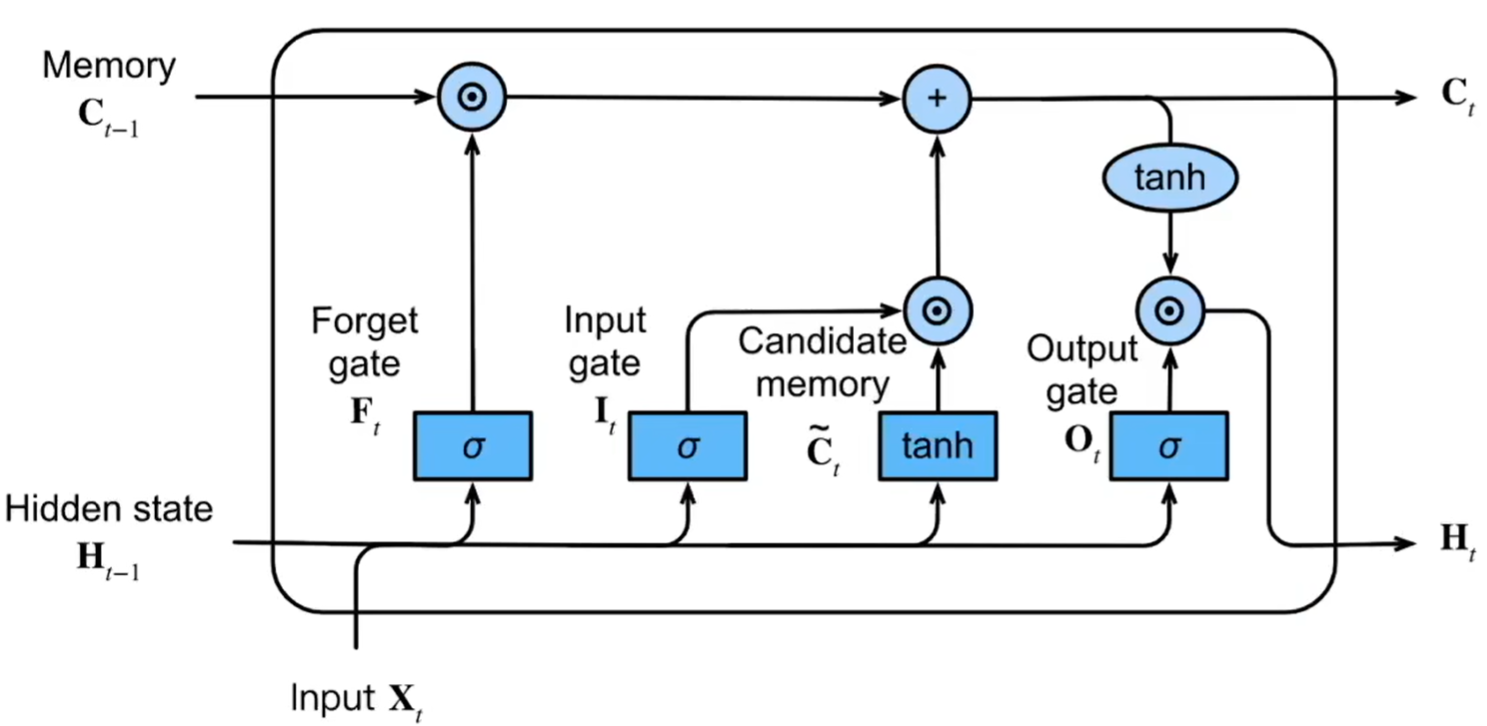
图 10.2: LSTM
LSTM的原理简单表示为下面几个公式。
记输入为\(X\),隐状态为\(H\),记忆元为\(C\),输入门为\(I\),遗忘门为\(F\),输出门为\(O\),则有
记忆元代表长期记忆,隐状态代表短期记忆
\[ \begin{aligned} I_t &= \sigma (X_tW_{xi}+H_{t-1}W_{hi}+b_i) \\ F_t &= \sigma (X_tW_{xf}+H_{t-1}W_{hf}+b_f) \\ O_t &= \sigma (X_tW_{xo}+H_{t-1}W_{ho}+b_o) \\ \tilde C_t &= \tanh(X_tW_{xc}+H_{t-1}W_{hc}+b_c) \\ C_t &= F_t \odot C_{t-1} + I_t \odot \tilde C_t \\ H_t &= O_t \odot \tanh (C_t) \end{aligned} \]
其中\(W,b\)分别代表权重与偏置,\(\sigma\)表示sigmoid函数,值域为[0,1],代表着信息剩余的比例,\(\tanh\)表示双曲正切函数,值域为[-1,1],代表着信息的大小及方向。
简单来看,\(X\)和\(H\)是对短期内的信息进行加工,然后将其上传到长期记忆中,而长期记忆也会遗忘部分信息,因此更新后的长期记忆表现为剩余的长期记忆与短期信息的和。而短期记忆又是长期记忆部分的一部分,并且会受到长期记忆的影响,因此\(H\)又可以由\(C\)产生。在这个过程中,就由输入门、遗忘门和输出门来控制信息损耗的比例。
10.4.2 示例
import torch
import torch.nn as nn
import numpy as np
from torch.utils.data import Dataset, DataLoader
# 设置随机种子以确保结果可复现
torch.manual_seed(42)
np.random.seed(42)
# 1. 生成正弦波数据
total_length = 1000
time_steps = np.linspace(0, 20 * np.pi, total_length)
data_sequence = np.sin(time_steps) + np.random.normal(0, 0.1, total_length)
# 2. 划分训练集和测试集
split_idx = int(total_length * 0.8) # 80%训练集,20%测试集
train_data = data_sequence[:split_idx]
test_data = data_sequence[split_idx:]
# 3. 创建序列数据集类
class SequenceDataset(Dataset):
def __init__(self, data, seq_length=20):
self.data = torch.FloatTensor(data)
self.seq_length = seq_length
def __len__(self):
return len(self.data) - self.seq_length
def __getitem__(self, idx):
input_seq = self.data[idx:idx+self.seq_length]
target = self.data[idx+self.seq_length]
return input_seq.view(self.seq_length, 1), target.view(1) # 添加特征维度
# 创建数据集和数据加载器
seq_length = 20
batch_size = 32
# 训练集
train_dataset = SequenceDataset(train_data, seq_length)
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True, drop_last=True)
# 测试集
test_dataset = SequenceDataset(test_data, seq_length)
test_loader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False, drop_last=True)
# 4. 定义LSTM模型
class LSTMModel(nn.Module):
def __init__(self, input_size=1, hidden_size=32, output_size=1, num_layers=1):
super().__init__()
self.num_layers = num_layers
self.hidden_size = hidden_size
# LSTM层
self.lstm = nn.LSTM(
input_size=input_size, # 默认为1即时序的自回归结构
hidden_size=hidden_size,
num_layers=num_layers,
batch_first=True
)
# 输出层
self.linear = nn.Linear(hidden_size, output_size)
def forward(self, x, hidden=None):
# 初始化隐藏状态
h0 = torch.zeros(self.num_layers, x.size(0), self.hidden_size).to('cuda')
c0 = torch.zeros(self.num_layers, x.size(0), self.hidden_size).to('cuda')
hidden = (h0, c0)
# 前向传播LSTM
# 需要将输入形状调整为 [batch, seq_len, features]
x = x.reshape(x.size(0), -1, 1) if x.dim() == 2 else x
# out表示LSTM最后一层所有时间步的输出
# hidden表示LSTM所有层在最后一个时间步的最终状态
out, hidden = self.lstm(x, hidden)
# 只取最后一个时间步的输出(batch, seq, features)
out = self.linear(out[:, -1, :])
return out, hidden
# 5. 实例化模型
input_size = 1
hidden_size = 64
output_size = 1
num_layers = 1
model = LSTMModel(input_size, hidden_size, output_size, num_layers)
# 将模型移到GPU上
model.to('cuda')
# 6. 定义损失函数和优化器
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
# 7. 训练模型
num_epochs = 50
train_losses = []
test_losses = []
for epoch in range(num_epochs):
# --- 训练阶段 ---
model.train()
epoch_train_loss = 0.0
for inputs, targets in train_loader:
# 输入形状: [batch_size, seq_length, 1]
# 目标形状: [batch_size, 1]
optimizer.zero_grad()
inputs, targets = inputs.to('cuda'), targets.to('cuda')
# 前向传播
outputs, _ = model(inputs)
loss = criterion(outputs, targets)
# 反向传播和优化
loss.backward()
optimizer.step()
epoch_train_loss += loss.item()
# 计算平均训练损失
avg_train_loss = epoch_train_loss / len(train_loader)
train_losses.append(avg_train_loss)
# --- 测试阶段 ---
model.eval()
epoch_test_loss = 0.0
with torch.no_grad():
for inputs, targets in test_loader:
inputs, targets = inputs.to('cuda'), targets.to('cuda')
outputs, _ = model(inputs)
loss = criterion(outputs, targets)
epoch_test_loss += loss.item()
# 计算平均测试损失
avg_test_loss = epoch_test_loss / len(test_loader)
test_losses.append(avg_test_loss)
# 每5个epoch打印一次进度
if (epoch+1) % 5 == 0 or epoch == 0:
print(f"Epoch [{epoch+1}/{num_epochs}], Train Loss: {avg_train_loss:.6f}, Test Loss: {avg_test_loss:.6f}")说明:
对于时序数据,给定t个数据后,t+1时刻的值即为响应变量。除了目标变量的自回归结构,还可以添加其他预测变量,记得要修改
input_size。关于h和c的初始状态,绝大部分场景下都需要进行重置,即不同序列之间的初始状态是独立的。同时,初始状态也不是需要学习的参数,除特殊任务外,一般都无需设置梯度。
如果要进行预测,则需要根据特定步长的窗口序列来预测下一时刻的目标值。单步预测直接让全连接层的输出维度为1;多步预测可以让全连接层的输出维度为目标维度,这等价于把未来步间的依赖压缩在最后的隐状态里,亦或者采取滚动预测的方式进行多步输出;除此之外,可考虑Seq2Seq的方法进行多步预测。