8.5 Cox比例风险模型

对于数据\(X_i=(X_{i1},\dots, X_{ip})^T\)，风险函数被定义为

\[ h_i(t)=h_0(t)\exp\{x_{i1}\beta_1+\dots+x_{ip}\beta_p\}=h_0(t)e^{X_i^T\beta} \tag{8.66} \]

其中\(h_0(t)\)被称为基线风险函数。

截距项被归到\(h_0(t)\)里了

考虑\(h_i(t|x)=h_0(t)e^{x_{i1}\beta_1}\)，称

\[ \frac{h_i(t|x+1)}{h_i(t|x)}=\frac{h_0(t)e^{x_{i1}\beta_1}e^{\beta_1}}{h_0(t)e^{x_{i1}\beta_1}}=e^{\beta_1} \tag{8.67} \] 这样的关系为“比例”关系。

8.5.1 偏对数似然函数

现有数据\((T_i,\delta_i, Z_i)\)，其中\(T_i\)表示记录的生存时间，\(\delta_i\)表示删失状态（1为非删失，0为删失），\(Z_i\)表示协变量。

回顾式(8.15)，写出Cox比例风险模型的似然函数。

\[ \begin{aligned} L(\theta)&=\prod_{i=1}^n \{f(\tau_i)\}^{\delta_i}\{S(\tau_i)\}^{1-\delta_i} \\ &= \prod_{i=1}^n \{h(\tau_i)\}^{\delta_i}S(\tau_i) \\ &= \prod_{i=1}^n [\{h_0(\tau_i)\exp(\beta^TZ_i)\}^{\delta_i}\exp\{-H_0(\tau_i)\exp(\beta^TZ_i)\}] \\ &= [\prod_{i=1}^n \{h_0(\tau_i)\exp(\beta^TZ_i)\}^{\delta_i}][\prod_{i=1}^n\exp\{-H_0(\tau_i)\exp(\beta^TZ_i)\}] \\ &= [\prod_{j=1}^D h_0(\tau_j)\exp(\beta^TZ_{(j)})] \exp\{-\sum_{i=1}^n\sum_{t_j \leq T_i}h_0(\tau_j)\exp(\beta^TZ_i)\} \\ &= [\prod_{j=1}^D h_0(\tau_j)\exp(\beta^TZ_{(j)})] \exp\{-\sum_{j=1}^D\sum_{i \in R_j}h_0(\tau_j)\exp(\beta^TZ_i)\} \end{aligned} \]

\(h(t)=\frac{f(t)}{S(t)},\; S(t)=\exp\{-H(t)\}\)

D表示非删失的对象数，指数处的\(\delta_i\)等价于就是对非删失的对象累乘

\(H_0(t)=\int_0^t h_0(x)dx\)，在实际中就是对不同死亡时刻的\(h_0(\tau)\)累加

\(R_j\)表示\(T_i \geq T_j\)的\(i\)的集合

---

8.5.2 Regularization Paths for Cox’s Proportional Hazards Model via Coordinate Descent

下面的内容是对Simon等人^[1]论文的复现。

观测对象的数据结构为\((y_i,x_i,\delta_i)\)，分别表示生存时间、自变量向量、生存结局。其中\(\delta_i\)取值为1: failure time或0: censoring time。将\(\delta=1\)的failure time进行排序得到\(t_1 \leq t_2 \leq \cdots \leq t_m\)。

在有结点情况时才有可能取到等号

8.5.2.1 推导

以下内容为个人推导，与原文略有出入

1. 无结点情况

\[ L(\beta)=\prod_{i=1}^m \frac{e^{x_{j(i)}^T\beta}}{\sum_{j \in R_i }e^{x_j^T\beta}} \]

其中\(R_i\)表示\(t_i \leq y_j\)的\(j\)的集合，\(j(i)\)表示第\(i\)个failure time对应的观测对象\(j\)。

\[ \frac{2}{n}l(\beta)=\frac{2}{n}\begin{bmatrix}\sum_{i=1}^mx_{j(i)}^T\beta-\sum_{i=1}^m\log(\sum_{j \in R_i}e^{x_j^T\beta})\end{bmatrix} \]

这里的1/n相当于是权重，2是为了消掉泰勒展开中的1/2

令\(\eta=X\beta\)，对对数似然函数进行二阶泰勒展开

\[ \begin{aligned} l(\beta)&\approx l(\tilde \beta)+(\beta-\tilde \beta)^T\dot l(\tilde \beta)+(\beta-\tilde \beta)^T\ddot l(\tilde \beta)(\beta-\tilde \beta)/2 \\ &=l(\tilde \beta)+(X\beta-\tilde \eta)^Tl'(\tilde \eta)+(X\beta-\tilde \eta)^Tl''(\tilde \eta)(X\beta-\tilde \eta)/2 \end{aligned} \]

其中

\[ \frac{\partial l(\eta)}{\partial \beta}=(X^T)_{p \times n}l'(\eta)_{n \times 1}=\dot l(\beta)_{p \times1} \]

\((X_{\cdot k})^Tl'(\eta)=\dot l(\beta)_k\)

整理可得

\[ l(\beta)\approx\frac{1}{2}(z(\tilde \eta)-X\beta)^Tl''(\tilde \eta)(z(\tilde \eta)-X\beta)+C(\tilde \eta,\tilde \beta)\\ z(\tilde \eta)=\tilde \eta-l''(\tilde \eta)^{-1}l'(\tilde \eta) \]

经检验，原文该表达式没错

则

\[ \frac{2}{n}l(\beta)\approx\frac{1}{n}(z(\tilde \eta)-X\beta)^Tl''(\tilde \eta)(z(\tilde \eta)-X\beta)+\frac{2}{n}C(\tilde \eta,\tilde \beta) \]

原文指出，为了计算方便，仅取黑塞矩阵的对角线元素而无视其他元素，其余元素对最终结果的影响也较小。

故目标函数为

\[ M(\beta)=-\frac{1}{n}\sum_{i=1}^nw(\tilde \eta)_i(z(\tilde \eta)_i-x_i^T\beta)^2+\lambda(\alpha\sum_{k=1}^p|\beta_k|+\frac{1}{2}(1-\alpha)\sum_{k=1}^p\beta_k^2) \]

其中\(w(\tilde \eta)_i\)是\(l''(\tilde \eta)\)的第\(i\)个对角线元素。

由于是最小化，对数似然函数得添负号

下面推导\(w(\eta)_i\)及\(z(\eta)_i\)的具体表达式

\[ l(\eta)=\sum_{i=1}^m (\eta_{j(i)}-\log(\sum_{j \in R_i}e^{\eta_j}))=\sum_{i=1}^m \eta_{j(i)}-\sum_{i=1}^m \log(\sum_{j \in R_i}e^{\eta_j}) \]

对\(\eta_k\)求偏导

\[ l'(\eta)_k=\delta_k-\sum_{i=1}^m \frac{e^{\eta_k}\textrm{I}_{\{y_k \geq t_i\}}}{\sum_{j \in R_i}e^{\eta_j}}=\delta_k-\sum_{i \in C_k}(\frac{e^{\eta_k}}{\sum_{j \in R_i}e^{\eta_j}}) \]

由于是对\(\eta_k\)求偏导，因此在\(\sum_{i=1}^m \eta_{j(i)}\)中，若有\(\eta_k\)则为1，反之为0。也就是说，只要\(y_k\)是failure time就为1，是删失数据即为0，等价于\(\delta_k\)。而对于给定的\(i\)，\(\eta_k\)不一定在\(\sum_{j \in R_i}e^{\eta_j}\)中，因此可根据\(R_i\)的定义添加示性函数。综合考虑\(\sum_{i=1}^m\)和\(\textrm{I}_{\{y_k \geq t_i\}}\)即可发现，\(\eta_k\)仅出现在\(y_k \geq t_i\)的\(i\)的集合中，也就是\(C_k\)的定义。

\[ \begin{aligned} l''(\eta)_{kk}&=-[e^{\eta_k} \cdot \sum\limits_{i \in C_k}\frac{1}{\sum_{j \in R_i}e^{\eta_j}}+e^{\eta_k}(-\sum_{i \in C_k}\frac{e^{\eta_k}}{(\sum_{j \in R_i}e^{\eta_j})^2})] \\ &=-\sum_{i \in C_k}\frac{e^{\eta_k}\sum_{j \in R_i}e^{\eta_j}-(e^{\eta_k})^2}{(\sum_{j \in R_i}e^{\eta_j})^2} \end{aligned} \]

当\(\sum_{i=1}^m\)转化为\(\sum_{i \in C_k}\)后，此时\(i\)对应的\(R_i\)中必定包含\(\eta_k\)，因此不用再加示性函数。

\(w(\tilde \eta)_k\)显然小于等于0，因为\(R_i\)中必定包含索引\(k\)

\[ z(\tilde \eta)_k=\tilde \eta_k-\frac{l'(\tilde \eta)_k}{l''(\tilde \eta)_{kk}}=\tilde \eta_k-\frac{\delta_k-\sum\limits_{i \in C_k}(\frac{e^{\eta_k}}{\sum_{j \in R_i}e^{\eta_j}})}{w(\tilde \eta)_k} \]

事实上，这里有一个致命的错误。当\(y_k \lt t_1\)时，\(C_k\)为空集，对应的\(w(\tilde \eta)_k=0\)，不能取倒数！

之后，对\(\beta_k\)求偏导

\[ \frac{\partial M}{\partial \beta_k}=\frac{2}{n}\sum_{i=1}^nw(\tilde \eta)_ix_{ik}(z(\tilde \eta)_i-x_i^T\beta)+\lambda\alpha\cdot\textrm{sgn}(\beta_k)+\lambda(1-\alpha)\beta_k \]

对于这个分子上的2，可以将其并到\(\lambda\)中从而忽略掉这个2，毕竟\(\lambda\)是数据驱动的参数。

令偏导为0，可得

\[ \frac{1}{n}\sum_{i=1}^nw_ix_{ik}(z_i-\sum_{j \neq k}x_{ij}\beta_j)-\frac{1}{n}\sum_{i=1}^nw_ix_{ik}^2\beta_k+\lambda\alpha\cdot \textrm{sgn}(\beta_k)+\lambda(1-\alpha)\beta_k=0 \]

行宽有限，这里简记\(w(\tilde \eta)_i=w_i\)、\(z(\tilde \eta)_i=z_i\)

再次强调，这里的1/n事实上就是权重，应该把\(w_i/n\)看出一个整体

此时可将不含\(\beta_k\)的第一项记作常数\(C\)，把后面的三项记作关于\(\beta_k\)的函数\(f(\beta_k)\)

\[ f(\beta_k)=(\lambda(1-\alpha)-\frac{1}{n}\sum_{i=1}^nw_ix_{ik}^2)\beta_k+\lambda\alpha\cdot\textrm{sgn}(\beta_k) \]

由于\(w_i \leq 0\)，且\(f(\beta_k)\)为奇函数，则其图像大概为

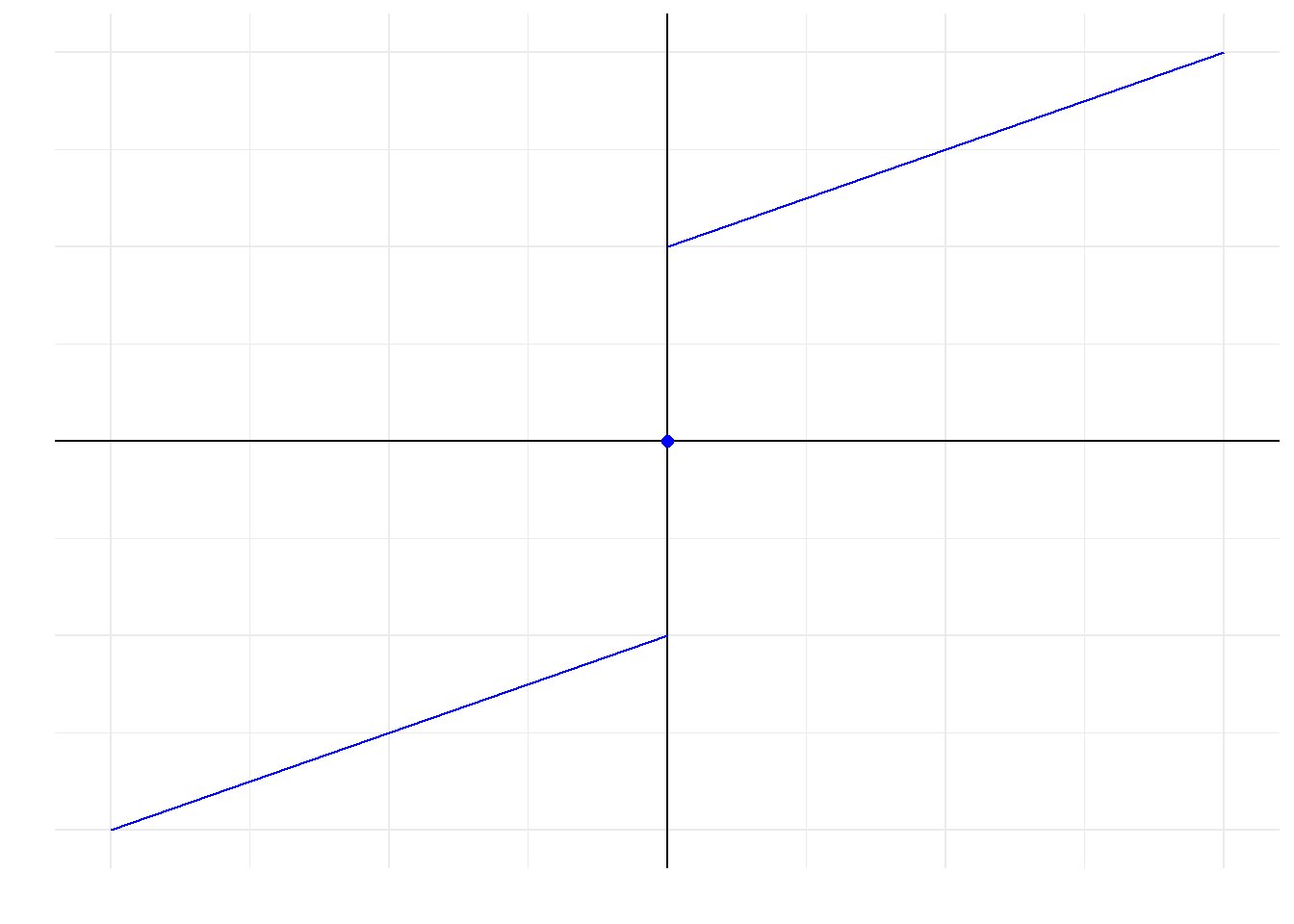
图 8.9: 函数图

则该问题就转化为对\(C\)进行分类讨论，看看\(f(\beta_k)\)什么时候和横轴相交，求出相交时的横坐标即可。思路已经有了，这里就不展开说了，得到结果如下所示

\[ \hat\beta_k=-\frac{\textrm{S}(\frac{1}{n}\sum_{i=1}^nw_ix_{ik}(z_i-\sum_{j \neq k}x_{ij}\beta_j),\lambda\alpha)}{-\frac{1}{n}\sum_{i=1}^nw_ix_{ik}^2+\lambda(1-\alpha)} \]

其中\(\textrm{S}(x,\lambda)=\textrm{sgn}(x)(|x|-\lambda)_+\)。

2. 有结点情况

有结点情况相较无结点情况就是多了权重，其余步骤都是一样的。

\[ L(\beta)=\prod_i^m\frac{\exp{(\sum_{j \in D_i}\omega_j\eta_j})}{(\sum_{j \in R_i}\omega_je^{\eta_j})^{d_i}} \]

其中\(D_i\)表示结点为\(t_i\)的集合，\(\omega_j\)表示权重，\(d_i=\sum_{j \in D_i}\omega_j\)。

对数似然函数为

\[ l(\beta)=\sum_i^{m}[(\sum_{j \in D_i}\omega_j\eta_j)-d_i\log(\sum_{j \in R_i}\omega_je^{\eta_j})] \]

对\(\eta_k\)求一阶导及二阶导

\[ l'(\eta)_k=\delta_k\omega_k-\sum_{i \in C_k}d_i\frac{\omega_ke^{\eta_k}}{\sum_{j \in R_i}\omega_je^{\eta_j}} \]

\[ l''(\eta)_{kk}=-\sum_{i \in C_k}d_i\frac{\omega_ke^{\eta_k}(\sum_{j \in R_i}\omega_je^{\eta_j})-(\omega_ke^{\eta_k})^2}{(\sum_{j \in R_i}\omega_je^{\eta_j})^2} \]

同样没有解决\(w(\eta)_k\)可能为0的问题。

你可以试着将其代入到无结点的情况下，也就是把\(\omega_j=d_i=1/n\)带进去，就会发现无结点情况下的那个1/n就是权重，应该把那个1/n并到\(l''(\tilde \eta)\)中，这样无结点和有结点就一致了

则

\[ z(\tilde \eta)_k=\tilde \eta_k-\frac{\delta_k\omega_k-\sum_{i \in C_k}d_i\frac{\omega_ke^{\eta_k}}{\sum_{j \in R_i}\omega_je^{\eta_j}}}{w(\tilde \eta)_k} \]

\(\hat\beta_k\)的表达式同无结点情形。

3. 收敛条件

定义\(D(\beta)\)为

\[ D(\beta)=2(l_{saturated}-l(\beta)) \]

则

\[ D_{null}=D(0)=2(l_{saturated}-l_{null}) \]

收敛条件为

\[ D(\beta_{current})-D_{null} \geq 0.99D_{null} \]

特别地，原文提供了简单的计算公式。在无结点情况下

\[ l_{saturated}=0\\ \]

\[ l_{null}=-\sum_{i=1}^m \log|R_i| \]

在有结点情况下

\[ l_{null}=-\sum_{i=1}^m d_i \log(\sum_{j \in R_i}w_j) \]

\[ l_{saturated}=-\sum_{i=1}^m d_i \log(d_i) \]

8.5.2.2 自定义算法

由于当前技术难以缩减计算时间，故自定义算法暂且放弃“正则化路径”功能

# **************参数输入**************
# y：矩阵，要求第一列为观测时间，第二列为状态
# X：自变量矩阵
# weight：权重向量，长度同样本量
# beta_0：迭代的初始值
# lambda/alpha：正则化参数
# max.iter：最大迭代次数
# trace：是否展示迭代过程
cox_cd <- function(y, X, weight=NULL, beta_0=NULL, lambda, alpha, max.iter=100, trace = FALSE){
  # 设置输出对象
  outcome = list(
    weight = NULL,
    lambda = NULL,
    alpha = NULL,
    beta = NULL,
    D_null = NULL,
    D_current = NULL
  )
  outcome$lambda = lambda
  outcome$alpha = alpha
  
  status = y[,2]
  y = y[,1]
  n = length(y)
  
  failure_t = y[status==1] %>% unique() %>% sort()
  R = map(failure_t, ~which(y>=.))   #R_i
  C = map(y, ~which(failure_t<=.))   #C_k
  
  # 根据是否有ties运行不同代码
  if(length(y)==length(unique(y))){
    # 无结点
    weight = 1/n #原文无ties情况的1/n就是有ties情况下权重为1/n的情形
    outcome$weight = weight
    
    # log_likelihood_beta用于精度判断
    log_likelihood_beta <- function(beta){
      term_1 = as.numeric(status %*% X %*% beta)   #在无结点情况下，j(i)与status等价
      term_2 = map_vec(R, function(R_i){
        map_vec(R_i, ~exp(X[.,] %*% beta)) %>% sum() %>% log()
      }) %>% sum()
      result = term_1 - term_2
      result
    }
    
    # 初始化beta
    if(is.null(beta_0)){
      beta = rep(0,dim(X)[2])
    }else{
      beta = beta_0
    }
    
    D_null = 2 * map_vec(R, ~length(.) %>% log()) %>% sum()   #用于判断精度
    outcome$D_null = D_null
    
    for (i in 1:max.iter) {
      if(trace == TRUE) cat(paste0("-----第", i, "次迭代-----\n"))
      
      eta = X %*% beta
      eta = scale(eta, TRUE, FALSE) # 源码有这个，为了保持一致我也加上去了
      hessian = map2_vec(C, c(1:length(C)), function(C_k, k){
        # 计算w_k
        C_k = C_k
        k = k   # .y提供位置索引
        eta_k = as.numeric(eta[k,])
        exp_eta_k = exp(eta_k)
        exp_eta_k_2 = exp_eta_k^2
        w_k = map_vec(C_k, function(i){
          sum_exp_eta_Ri = map_vec(R[[i]], ~exp(eta[.,])) %>% sum()
          sum_exp_eta_Ri_2 = sum_exp_eta_Ri^2
          value = (exp_eta_k * sum_exp_eta_Ri - exp_eta_k_2) / sum_exp_eta_Ri_2
          value
        }) %>% sum()
        w_k = -weight * w_k   # 无结点情况的1/n就相当于是权重
        w_k
      })
      grad = map2_vec(C, c(1:length(C)), function(.x, .y){
        # 计算w_k
        C_k = .x
        k = .y   # .y提供位置索引
        eta_k = as.numeric(eta[k,])
        exp_eta_k = exp(eta_k)
        w_prior_k = map_vec(C_k, function(i){
          sum_exp_eta_Ri = map_vec(R[[i]], ~exp(eta[.,])) %>% sum()
          value = exp_eta_k / sum_exp_eta_Ri
          value
        }) %>% sum()
        w_prior_k
      })
      grad = weight * (status - grad)
      if(any(hessian==0)){
        if(trace == TRUE) cat('=====w_k中有零=====\n')
        hessian[which(hessian == 0)] = 0.0000001
      }
      z = eta - grad / hessian
      
      last_beta = beta
      # 坐标下降法
      for (k in 1:length(beta)) {
        denominator = as.numeric(hessian %*% X[,k]^2 + lambda * (1-alpha))
        numerator = as.numeric(t(diag(hessian) %*% X[,k]) %*% (z - X[,-k] %*% beta[-k]))
        numerator = sign(numerator) * max(abs(numerator), lambda * alpha)
        beta[k] = numerator/denominator
      }
      # 精度判断
      # 无ties情况下，l_saturated = 0
      D_current = -2 * log_likelihood_beta(beta)
      outcome$D_current = D_current
      
      # 和原文的收敛条件不同，感觉这样更符合逻辑，详见“自定义算法检验”
      if(D_null - D_current >= 0.99 * D_null){
        if(trace == TRUE){
          cat(paste0(beta, '\n'))
          cat('<<<<<满足精度要求>>>>>\n')
        }
        break
      }
      if(all(round(last_beta, 7) == round(beta, 7))){
        if(trace == TRUE){
          cat(paste0(beta, '\n'))
          cat('<<<<<系数不再更新>>>>>\n')
        }
        break
      }
      if(trace == TRUE) cat(paste0(beta,'\n'))
    }
    outcome$beta = beta
    
    return(outcome)
  }else{
    # 有ties
    if(is.null(weight)){
      weight = rep(1, n)/n   #若不指定权重，则默认为1/n
    }else{
      if(length(weight) == n){
        if(sum(weight) == 1){
          weight   #若权重和为1，则可以
        }else{
          weight = weight/sum(weight)   #若权重和不为1，则标准化
        }
      }else{
        cat('权重向量长度不匹配\n')
      }
    }
    outcome$weight = weight
    
    D = map(failure_t, ~which(y == . & status==1))
    d = map_vec(D, ~sum(weight[.]))
    # log_likelihood_beta用于精度判断
    log_likelihood_beta <- function(beta){
      term_1 = as.numeric(status %*% diag(weight) %*% X %*% beta)   #第一项等价于所有的failure time的加权和
      term_2 = map_vec(R, function(R_i){
        map_vec(R_i, ~weight[.] * exp(X[.,] %*% beta)) %>% sum() %>% log()
      }) %*% d
      result = term_1 - as.numeric(term_2)
      result
    }
    
    # 初始化beta
    if(is.null(beta_0)){
      beta = rep(0,dim(X)[2])
    }else{
      beta = beta_0
    }
    
    # 用于精度判断
    l_null = -map_vec(R, function(R_i){
      map_vec(R_i, ~weight[.]) %>% sum() %>% log()
    }) %*% d %>% as.numeric()
    l_saturated = -as.numeric(d %*% log(d))
    D_null = 2 * (l_saturated - l_null)
    outcome$D_null = D_null
    
    for (i in 1:max.iter) {
      if(trace == TRUE) cat(paste0("-----第", i, "次迭代-----\n"))
      
      eta = X %*% beta
      eta = scale(eta, TRUE, FALSE)   #源码有这个，为了保持一致我也加上去了
      hessian = map2_vec(C, c(1:length(C)), function(C_k, k){
        # 计算w_k
        C_k = C_k
        k = k   # .y提供位置索引
        eta_k = as.numeric(eta[k,])
        weight_exp_eta_k = weight[k] * exp(eta_k)
        weight_exp_eta_k_2 = (weight_exp_eta_k)^2
        w_k = map_vec(C_k, function(i){
          weight_sum_exp_eta_Ri = map_vec(R[[i]], ~weight[.] * exp(eta[.,])) %>% sum()
          weight_sum_exp_eta_Ri_2 = weight_sum_exp_eta_Ri^2
          value = d[i] * (weight_exp_eta_k * weight_sum_exp_eta_Ri - weight_exp_eta_k_2) / weight_sum_exp_eta_Ri_2
          value
        }) %>% sum()
        w_k = -w_k   #权重已经包含在w_k里面了
        w_k
      })
      grad = map2_vec(C, c(1:length(C)), function(.x, .y){
        # 计算w_k
        C_k = .x
        k = .y   # .y提供位置索引
        eta_k = as.numeric(eta[k,])
        weight_exp_eta_k = weight[k] * exp(eta_k)
        w_prior_k = map_vec(C_k, function(i){
          weight_sum_exp_eta_Ri = map_vec(R[[i]], ~weight[.] * exp(eta[.,])) %>% sum()
          value = d[i] * weight_exp_eta_k / weight_sum_exp_eta_Ri
          value
        }) %>% sum()
        w_prior_k = status[k] * weight[k]-w_prior_k
        w_prior_k
      })
      
      if(any(hessian==0)){
        if(trace == TRUE) cat('=====w_k中有零=====\n')
        hessian[which(hessian == 0)] = 0.0000001
      }
      z = eta - grad / hessian
      
      last_beta = beta
      for (k in 1:length(beta)) {
        denominator = as.numeric(hessian %*% X[,k]^2 + lambda * (1-alpha))
        numerator = as.numeric(t(diag(hessian) %*% X[,k]) %*% (z - X[,-k] %*% beta[-k]))
        numerator = sign(numerator) * max(abs(numerator), lambda * alpha)
        beta[k] = numerator/denominator
      }
      # 精度判断
      D_current = 2 * (l_saturated - log_likelihood_beta(beta))
      outcome$D_current = D_current
      
      if(D_null - D_current >= 0.99 * D_null){
        if(trace == TRUE){
          cat(paste0(beta, '\n'))
          cat('<<<<<满足精度要求>>>>>\n')
        }
        break
      }
      if(all(round(last_beta, 7) == round(beta, 7))){
        if(trace == TRUE){
          cat(paste0(beta, '\n'))
          cat('<<<<<系数不再更新>>>>>\n')
        }
        break
      }
      if(trace == TRUE) cat(paste0(beta,'\n'))
    }
    outcome$beta = beta
    
    return(outcome)
  }
}

8.5.2.3 自定义算法检验

模拟所用数据集来自glmnet包的data(CoxExample)数据集。

内容总结：

• 自定义算法的梯度向量、黑塞矩阵对角线元素与源码计算结果基本一致。其中黑塞矩阵对角线元素可能会出现0，因此为其加上非常小的数(0.0000001)。

• 对于收敛条件，对于无结点情况，自定义算法与原函数的结果完全一致，但在有结点情况则存在差异。同时有理由怀疑除了原文给出的收敛条件外，还有其他的收敛条件，并且原文的收敛条件可能有误。

• 对自定义算法随机选取初始值，发现均能收敛到相同结果，表明自定义算法具有一定的稳健性。但与原函数的结果还存在差异。

综上，自定义算法是对论文内容的复刻，因此在未提及的细节处必定与原函数存在差异，从而导致结果的差异。但此次复刻不失为一次有益的探索。

1. 梯度向量与黑塞矩阵

library(glmnet)
data(CoxExample)
X <- CoxExample[[1]][1:50,1:5]
y <- CoxExample[[2]][1:50,]
head(X)

##            [,1]       [,2]        [,3]       [,4]        [,5]
## [1,] -0.8767670 -0.6135224 -0.56757380  0.6621599  1.82218019
## [2,] -0.7463894 -1.7519457  0.28545898  1.1392105  0.80178007
## [3,]  1.3759148 -0.2641132  0.88727408  0.3841870  0.05751801
## [4,]  0.2375820  0.7859162 -0.89670281 -0.8339338 -0.58237643
## [5,]  0.1086275  0.4665686 -0.57637261  1.7041314  0.32750715
## [6,]  1.2027213 -0.4187073 -0.05735193  0.5948491  0.44328682

head(y)

##            time status
## [1,] 1.76877757      1
## [2,] 0.54528404      1
## [3,] 0.04485918      0
## [4,] 0.85032298      0
## [5,] 0.61488426      1
## [6,] 0.29860939      0

status = y[,2]
y = y[,1]
n = length(y)

failure_t = y[status==1] %>% sort()
R = map(failure_t, ~which(y>=.)) #R中每个元素对应原文的R_i
C = map(y, ~which(failure_t<=.))

# 无ties
weight = 1/n #原文无ties情况的1/n就是有ties情况下权重为1/n的情形
  
# 初始化beta
beta = rep(0,dim(X)[2])

eta = X %*% beta
eta = scale(eta, TRUE, FALSE)  #源码有这个中心化的操作，为了保持一致，这里也加上

# 梯度向量
my_grad = map2_vec(C, c(1:length(C)), function(.x, .y){
  # 计算w_k
  C_k = .x
  k = .y   # .y提供位置索引
  eta_k = as.numeric(eta[k,])
  exp_eta_k = exp(eta_k)
  w_prior_k = map_vec(C_k, function(i){
    sum_exp_eta_Ri = map_vec(R[[i]], ~exp(eta[.,])) %>% sum()
    value = exp_eta_k / sum_exp_eta_Ri
    value
  }) %>% sum()
  w_prior_k
})
my_grad = weight * (status - my_grad)

# 黑塞矩阵对角线元素
hessian = map2_vec(C, c(1:length(C)), function(C_k, k){
  # 计算w_k
  C_k = C_k
  k = k   # .y提供位置索引
  eta_k = as.numeric(eta[k,])
  exp_eta_k = exp(eta_k)
  exp_eta_k_2 = exp_eta_k^2
  w_k = map_vec(C_k, function(i){
    sum_exp_eta_Ri = map_vec(R[[i]], ~exp(eta[.,])) %>% sum()
    sum_exp_eta_Ri_2 = sum_exp_eta_Ri^2
    value = (exp_eta_k * sum_exp_eta_Ri - exp_eta_k_2) / sum_exp_eta_Ri_2
    value
  }) %>% sum()
  w_k = -weight * w_k   # 无结点情况的1/n就相当于是权重
  w_k
  })
my_hessian = hessian

下面是源码中关于梯度向量和黑塞矩阵的计算。

X <- CoxExample[[1]][1:50,1:5]
y <- CoxExample[[2]][1:50,]

fid <- function(x,index) {
  idup=duplicated(x)
  if(!any(idup)) list(index_first=index,index_ties=NULL)
  else {
    ndup=!idup
    xu=x[ndup]# first death times
    index_first=index[ndup]
    ities=match(x,xu)
    index_ties=split(index,ities)
    nties=sapply(index_ties,length)
    list(index_first=index_first,index_ties=index_ties[nties>1])
  }
}

w=rep(1,length(eta))
w=w/sum(w)
nobs <- nrow(y)
time <- y[, "time"]
d    <- y[, "status"]
eta <- scale(eta, TRUE, FALSE)
o <- order(time, d, decreasing = c(FALSE, TRUE))
exp_eta <- exp(eta)[o]
time <- time[o]
d <- d[o]
w <- w[o]
rskden <- rev(cumsum(rev(exp_eta*w)))
dups <- fid(time[d == 1],seq(length(d))[d == 1])
dd <- d
ww <- w
rskcount=cumsum(dd)
rskdeninv=cumsum((ww/rskden)[dd==1])
rskdeninv=c(0,rskdeninv)
grad <- w * (d - exp_eta * rskdeninv[rskcount+1])
grad[o] <- grad   #源码的梯度向量
rskdeninv2 <- cumsum((ww/(rskden^2))[dd==1])
rskdeninv2 <- c(0, rskdeninv2)
w_exp_eta <- w * exp_eta
diag_hessian <- w_exp_eta^2 * rskdeninv2[rskcount+1] - w_exp_eta * rskdeninv[rskcount+1]
diag_hessian[o] <- diag_hessian   #源码的黑塞矩阵对角线

梯度向量对比。

my_grad   #我的梯度向量

##  [1] -0.0014031776  0.0156521479 -0.0008699764 -0.0093888607  0.0141421764
##  [6] -0.0029439112  0.0000000000 -0.0404031776  0.0124726112 -0.0214031776
## [11]  0.0056201324  0.0163664336  0.0176275174 -0.0008699764 -0.0214031776
## [16] -0.0116179628 -0.0066578236  0.0024150042  0.0133421764 -0.0029439112
## [21]  0.0000000000 -0.0104414923  0.0186538332 -0.0029439112  0.0149114072
## [26] -0.0018461668 -0.0214031776  0.0195744681 -0.0054031776  0.0115635203
## [31] -0.0013461668 -0.0023724826  0.0106111393  0.0000000000  0.0070487038
## [36]  0.0191300236 -0.0214031776 -0.0029439112 -0.0004255319 -0.0204031776
## [41]  0.0170560888  0.0040816709 -0.0104031776  0.0005968224 -0.0304031776
## [46]  0.0095585077 -0.0023724826  0.0181538332  0.0083820372 -0.0029439112

grad      #源码的梯度向量

##  [1] -0.0014031776  0.0156521479 -0.0008699764 -0.0093888607  0.0141421764
##  [6] -0.0029439112  0.0000000000 -0.0404031776  0.0124726112 -0.0214031776
## [11]  0.0056201324  0.0163664336  0.0176275174 -0.0008699764 -0.0214031776
## [16] -0.0116179628 -0.0066578236  0.0024150042  0.0133421764 -0.0029439112
## [21]  0.0000000000 -0.0104414923  0.0186538332 -0.0029439112  0.0149114072
## [26] -0.0018461668 -0.0214031776  0.0195744681 -0.0054031776  0.0115635203
## [31] -0.0013461668 -0.0023724826  0.0106111393  0.0000000000  0.0070487038
## [36]  0.0191300236 -0.0214031776 -0.0029439112 -0.0004255319 -0.0204031776
## [41]  0.0170560888  0.0040816709 -0.0104031776  0.0005968224 -0.0304031776
## [46]  0.0095585077 -0.0023724826  0.0181538332  0.0083820372 -0.0029439112

黑塞矩阵对角线元素对比。

my_hessian    #我的黑塞矩阵对角线元素

##  [1] -0.0201293825 -0.0042256154 -0.0008510459 -0.0090531224 -0.0056785663
##  [6] -0.0028709660  0.0000000000 -0.0320793825 -0.0072783243 -0.0201293825
## [11] -0.0137285938 -0.0035368399 -0.0023158639 -0.0008510459 -0.0201293825
## [16] -0.0111576188 -0.0064465663 -0.0166764899 -0.0064465663 -0.0028709660
## [21]  0.0000000000 -0.0100503523 -0.0013158986 -0.0028709660 -0.0049389213
## [26] -0.0018033986 -0.0201293825 -0.0004164780 -0.0233293825 -0.0081460929
## [31] -0.0013158986 -0.0023158639 -0.0090531224  0.0000000000 -0.0124020632
## [36] -0.0008510459 -0.0201293825 -0.0028709660 -0.0004164780 -0.0320793825
## [41] -0.0028709660 -0.0151487122 -0.0270793825 -0.0183293825 -0.0270793825
## [46] -0.0100503523 -0.0023158639 -0.0018033986 -0.0111576188 -0.0028709660

diag_hessian  #源码的黑塞矩阵对角线元素

##  [1] -0.0201293825 -0.0042256154 -0.0008510459 -0.0090531224 -0.0056785663
##  [6] -0.0028709660  0.0000000000 -0.0320793825 -0.0072783243 -0.0201293825
## [11] -0.0137285938 -0.0035368399 -0.0023158639 -0.0008510459 -0.0201293825
## [16] -0.0111576188 -0.0064465663 -0.0166764899 -0.0064465663 -0.0028709660
## [21]  0.0000000000 -0.0100503523 -0.0013158986 -0.0028709660 -0.0049389213
## [26] -0.0018033986 -0.0201293825 -0.0004164780 -0.0233293825 -0.0081460929
## [31] -0.0013158986 -0.0023158639 -0.0090531224  0.0000000000 -0.0124020632
## [36] -0.0008510459 -0.0201293825 -0.0028709660 -0.0004164780 -0.0320793825
## [41] -0.0028709660 -0.0151487122 -0.0270793825 -0.0183293825 -0.0270793825
## [46] -0.0100503523 -0.0023158639 -0.0018033986 -0.0111576188 -0.0028709660

可见，二者基本一致。

当用my_grad==grad及my_hessian==diag_hessian比较是否一致时，小部分是FALSE，但单从展示的数值上来看，几乎是一致的，可见差异微乎其微。

需要注意的是，正如前面提到的，\(w(\tilde \eta)_k\)可能为0。无论是自定义算法还是源码都输出了0（第7,21,34个对角线元素），但源码的函数能够运行下去，而自定义算法则不行，说明原文遗漏了一些细节。

当\(y_k \lt t_1\)时，\(C_k\)即为空集，则对应的\(w(\tilde \eta)_k=0\)

即使删掉\(C_k\)为空集的观测对象，结果也与原函数不一致

鉴于此，为\(w(\tilde \eta)_k=0\)的元素加上非常小的数(0.0000001)以确保代码能够正确运行。

2. 收敛条件

原文中使用\(D(0)\)与\(D(\beta_{current})\)作为收敛条件。\(D(\cdot)\)的内核就是对数似然函数，不妨先确定自定义算法中关于对数似然函数的定义是否正确。

先考虑无结点的情况。此时\(l_{saturated}=0\)

用自定义算法中的log_likelihood_beta()函数计算\(D(0)\)

X <- CoxExample[[1]][1:50,1:5]
y <- CoxExample[[2]][1:50,]
log_likelihood_beta <- function(beta){
  term_1 = as.numeric(status %*% X %*% beta)   #在无结点情况下，j(i)与status等价
  term_2 = map_vec(R, function(R_i){
    map_vec(R_i, ~exp(X[.,] %*% beta)) %>% sum() %>% log()
  }) %>% sum()
  result = term_1 - term_2
  result
}

status = y[,2]
y = y[,1]
n = length(y)
failure_t = y[status==1] %>% unique() %>% sort()   #t_i
R = map(failure_t, ~which(y>=.))   #R_i
D_null <- (-2) * log_likelihood_beta(rep(0,5))
D_null

## [1] 145.1673

原函数也会输出\(D(0)\)

X <- CoxExample[[1]][1:50,1:5]
y <- CoxExample[[2]][1:50,]
source_result <- glmnet(X,y,family = 'cox', lambda=0.02, alpha=0.5)
source_result$nulldev

## [1] 145.1673

可见二者是一致的。

再看看\(D(\beta_{current})\)。原函数输出的结果中有dev.ratio一项，其值为\(dev.ratio = 1-D(\beta_{current})/D(0)\)。因此可根据dev.ratio及nulldev两项输出值计算\(D(\beta_{current})\)

# 原函数输出的D_current
source_result$nulldev - source_result$dev.ratio * source_result$nulldev

## [1] 132.0468

# 自定义算法log_likelihood_beta()函数输出的D_current
-2 * log_likelihood_beta(source_result$beta@x)

## [1] 132.0468

因此无论是\(D(0)\)还是\(D(\beta_{current})\)，均表明自定义算法中的log_likelihood_beta()是正确的。

注意，\(D(\beta_{current})=132\)，\(D(0)=145\)，根本没法满足原文的收敛条件。进一步地，对数据集进行随机抽样，看看原函数是否有按原文的收敛条件停止迭代。

set.seed(111)

result <- rep(NA, 100)

for (i in 1:100) {
  obs <- sample(1:1000,500)
  index <- sample(1:30,15)
  
  X <- CoxExample[[1]][obs,index]
  y <- CoxExample[[2]][obs,]
  
  source_result <- glmnet(X,y,family = 'cox', lambda=0.02, alpha=0.5)
  
  D_beta = source_result$nulldev - source_result$dev.ratio * source_result$nulldev
  D_null = source_result$nulldev
  
  convergence = D_beta-D_null >= 0.99*D_null
  result[i] = convergence
}
sum(result)

## [1] 0

可见，在100次的随机抽样中，原函数没有一次根据原文所给的收敛条件停止迭代。下面，再来细看原文的收敛条件

\[ \begin{aligned} D(\beta_{current})-D_{null} &\geq 0.99D_{null} \\ 2(l_{saturated}-l(\beta))-2(l_{saturated}-l_{null}) &\geq 0.99 \ast 2(l_{saturated}-l_{null}) \\ l_{null}-l(\beta) &\geq 0.99(l_{saturated}-l_{null}) \\ \frac{l_{null}-l(\beta)}{l_{saturated}-l_{null}} &\geq 0.99 \end{aligned} \]

注意到，\(l_{saturated}\)是对数似然函数在理论上的最大值，故\(l_{saturated}-l_{null} \gt 0\)。一般来说，如果引入\(X\beta\)有助于解释的话，那么\(l(\beta) \gt l_{null}\)，则原文的收敛条件必不可能满足。若分子改为\(l(\beta)-l_{null}\)则较为合理，表示引入\(X\beta\)后多解释的那一部分信息，那么收敛条件就变为考察这部分信息是否占\(l_{saturated}-l_{null}\)的绝大部分。

自定义算法的收敛条件已按\(D_{null}-D(\beta_{current}) \geq 0.99D_{null}\)设置

既然原文给出的收敛条件有问题，并且随机抽样的结果也表明不符合给出的收敛条件，但原函数却收敛了，说明原函数还设置了其他收敛条件。鉴于此，自定义算法会在前后两次\(\hat \beta\)的变化微乎其微时停止迭代。

“微乎其微”是指保留7位小数后相等

而对于有结点的情况，则有点差异。

X <- CoxExample[[1]][1:50,1:5]
y <- CoxExample[[2]][1:50,]
y[36:50,] <- y[1:15,]   #设置重复数据

status = y[,2]
y = y[,1]
n = length(y)
weight = rep(1, n)/n

failure_t = y[status==1] %>% unique() %>% sort()
R = map(failure_t, ~which(y>=.))   #R_i

D = map(failure_t, ~which(y == . & status==1))
d = map_vec(D, ~sum(weight[.]))
# log_likelihood_beta用于精度判断
log_likelihood_beta <- function(beta){
  term_1 = as.numeric(status %*% diag(weight) %*% X %*% beta)   #第一项等价于所有的failure time的加权和
  term_2 = map_vec(R, function(R_i){
    map_vec(R_i, ~weight[.] * exp(X[.,] %*% beta)) %>% sum() %>% log()
  }) %*% d
  result = term_1 - as.numeric(term_2)
  result
}

# 自定义算法
l_null = log_likelihood_beta(rep(0,5))
l_null

## [1] 0.5402271

# 原文提到的简化算法
l_null_simple = -map_vec(R, function(R_i){
      map_vec(R_i, ~weight[.]) %>% sum() %>% log()
    }) %*% d %>% as.numeric()
l_null_simple

## [1] 0.5402271

原文提到的关于\(l_{null}\)的快速算法和自定义算法中的log_likelihood_beta(0)函数结果一致。接着计算\(D_{null}\)

# 自定义算法
l_saturated = -as.numeric(d %*% log(d))
D_null = 2 * (l_saturated - l_null)
D_null

## [1] 2.387955

D_null * 50

## [1] 119.3977

和原函数的\(D_{null}\)进行对比

X <- CoxExample[[1]][1:50,1:5]
y <- CoxExample[[2]][1:50,]
y[36:50,] <- y[1:15,]   #设置重复数据

source_result <- glmnet(X,y,family = 'cox', lambda=0.02, alpha=0.5)
source_result$nulldev

## [1] 119.3977

source_result$beta

## 5 x 1 sparse Matrix of class "dgCMatrix"
##            s0
## V1  0.1261175
## V2 -0.3690040
## V3  .        
## V4  0.1141002
## V5 -0.3313418

自定义算法输出的\(\beta\)向量为

0.18386651 -0.43987813 -0.03533338 0.13130503 -0.36330350

自定义算法得到的\(D_{null}\)与原函数输出的结果差了50倍。既然原文提到的关于\(l_{null}\)的快速算法和自定义算法中的log_likelihood_beta(0)函数结果一致，那么说明原函数暗中调整了倍数。因此，对于收敛条件的判定，如果\(D_{null}\)与\(D(\beta_{current})\)都做了倍数调整的话，那么结果也是不变的，所以无需过分在意这里的倍数差异。另外，原函数没有输出第三个变量的\(\hat \beta\)，至少能看出来自定义算法和原函数还是存在差异（毕竟原函数没有输出第三个变量的系数，但自定义函数可以），归根结底还是论文提供的细节太少了。

3. 随机化初始值

上述自定义算法的结果都是基于\(\beta=0\)的初始值开始迭代，下面通过随机化初始值看看自定义算法的稳健性。

X <- CoxExample[[1]][1:50,1:5]
y <- CoxExample[[2]][1:50,]
set.seed(111)
for (i in 1:10) {
  cat(paste0("----------第", i, "次迭代----------"))
  cat('\n')
  beta_0 = runif(5,min=0,max=1)
  my_result = cox_cd(y, X, beta_0 = beta_0, lambda=0.02, alpha=0.5, trace = FALSE)
  cat(my_result$beta)
  cat('\n')
}

## ----------第1次迭代----------
## 0.395017 -0.8420384 -0.1444031 0.363653 -0.5357859
## ----------第2次迭代----------
## 0.395017 -0.8420384 -0.1444031 0.363653 -0.5357859
## ----------第3次迭代----------
## 0.395017 -0.8420384 -0.1444031 0.363653 -0.5357859
## ----------第4次迭代----------
## 0.395017 -0.8420384 -0.1444031 0.363653 -0.5357859
## ----------第5次迭代----------
## 0.395017 -0.8420384 -0.1444031 0.363653 -0.5357859
## ----------第6次迭代----------
## 0.395017 -0.8420385 -0.1444031 0.363653 -0.5357859
## ----------第7次迭代----------
## 0.395017 -0.8420385 -0.1444031 0.363653 -0.5357859
## ----------第8次迭代----------
## 0.395017 -0.8420384 -0.1444031 0.363653 -0.5357859
## ----------第9次迭代----------
## 0.395017 -0.8420384 -0.1444031 0.363653 -0.5357859
## ----------第10次迭代----------
## 0.395017 -0.8420384 -0.1444031 0.363653 -0.5357859

source_result <- glmnet(X,y,family = 'cox', lambda=0.02, alpha=0.5)
source_result$beta@x #原函数的结果

## [1]  0.2800404 -0.6870509 -0.1062398  0.3150430 -0.4588579

据此可知自定义算法具有一定的稳健性，但与原函数的结果存在一定差异。

References

[1]

SIMON N. FRIEDMAN J H. HASTIE T. 等. Regularization paths for Cox’s proportional hazards model via coordinate descent[J]. Journal of Statistical Software, 2011, 39: 1-13.