16.2 单变量选择
在Fan & Li[14]的论文中提到一个好的惩罚函数产生的估计应该满足如下三条性质:
无偏性
当真实系数足够大时,对它的估计应当是无偏的。
稀疏性
估计结果应当是分段的,当系数估计值较小时应当被设置为0。
连续性
估计结果应当是连续的。
文章[14]中提到在原点奇异即可满足稀疏性和连续性。
16.2.1 Lasso
glmnet包的glmnet()函数
Tibshirani[15]提出的\(Lasso\)是用于变量选择的经典方法之一。其惩罚函数如下所示
\[ P_\lambda(\beta)=\lambda|| \beta ||_1=\lambda\sum\limits_{i=1}^p |\beta_i| \tag{16.8} \]
式(16.8)表明\(Lasso\)就是在目标函数中添加了\(L_1\)正则项。\(L_1\)正则项的\(contour\)图如图16.1所示,函数图如图16.7所示,3D图如图16.3所示。
\(Lasso\)的解为
\[ \hat{\beta_j}=sgn(z)(|z|-\lambda)_{+} \tag{16.9} \] 其中\(z\)表示最小二乘估计的解,下同。解的图像如图16.8所示。由图可知,该解满足连续性和稀疏性,但不满足无偏性。
下面的优缺点来自各个方法的原文献及相关文献,下同。
优点
- 通过\(L_1\)正则化项,可以将一些系数压缩到零,从而实现变量选择
- 在高维数据中表现良好,尤其在信噪比大的情况下。
缺点
- \(Lasso\)可能会引入较大的偏差,特别是在样本量不充足时。
- \(Lasso\)不满足\(Oracle\)性质,即它不能在变量选择上与已知真实模型的情况进行比较。
- 需要选择合适的正则化参数
16.2.2 Hard & Soft Threshold
\(Hard \; Threshold\)(硬阈值)与\(Soft \; Threshold\)(软阈值)初见于文献[16]。解的形式为
\[ \begin{aligned} \hat\beta_{H}&=zI(|z|>\lambda) \\ \hat\beta_{S}&=sgn(z)(|z|-\lambda)_{+} \end{aligned} \tag{16.10} \]
可以发现,软阈值的解与\(Lasso\)的解一模一样。Tibshirani在其文章[15]中也指出了这种联系。
在Fan & Li[14]的文章中给出了当惩罚函数为\(P_\lambda(|\theta|)=\lambda^2-(|\theta|-\lambda)^2I(|\theta|-\lambda)\)时硬阈值的惩罚函数及解的图像,分别如图16.7、图16.8所示。
由图可知,硬阈值的解满足无偏性、稀疏性,不满足连续性。软阈值的解满足连续性、稀疏性,不满足无偏性。
16.2.3 SCAD
ncvreg包的ncvreg()函数
Fan & Li[14]提出的\(SCAD\)惩罚函数很好地弥补了硬阈值和软阈值的不足,同时满足无偏性、稀疏性和连续性。更进一步地,文中证明了\(SCAD\)法具有\(Oracle\)性质。
\(Oracle\)性质:(1)能正确选择模型,即对真实为零的系数,方法能将其估计值压缩到零,对真实非零的系数,方法能正确识别对应的变量;(2)真实非零系数的估计值是无偏或近似无偏的,且具有渐进正态性。
原文从导数的角度给出了\(SCAD\)函数的定义
\[ P'_\lambda(\theta)=\lambda\{I(\theta\leq\lambda)+\frac{(a\lambda-\theta)_+}{(a-1)\lambda}I(\theta \gt \lambda)\}, \; a\gt2 \; \& \; \theta \gt 0 \tag{16.11} \]
并且也给出了解的表达式
\[ \hat{\theta}= \begin{cases} sgn(z)(|z|-\lambda)_+, & |z| \leq 2\lambda \\ \{(a-1)z-sgn(z)a\lambda\}/(a-2), & 2\lambda \lt |z| \leq a\lambda \\ z, & |z| \gt a\lambda \end{cases} \tag{16.12} \]
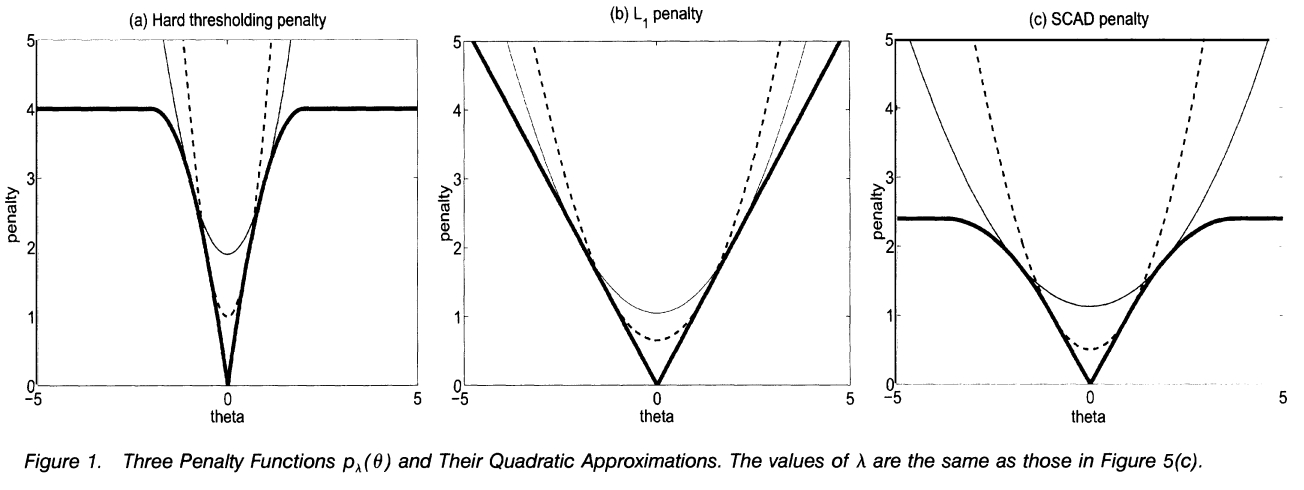
图 16.7: 硬阈值、软阈值和SCAD的惩罚函数
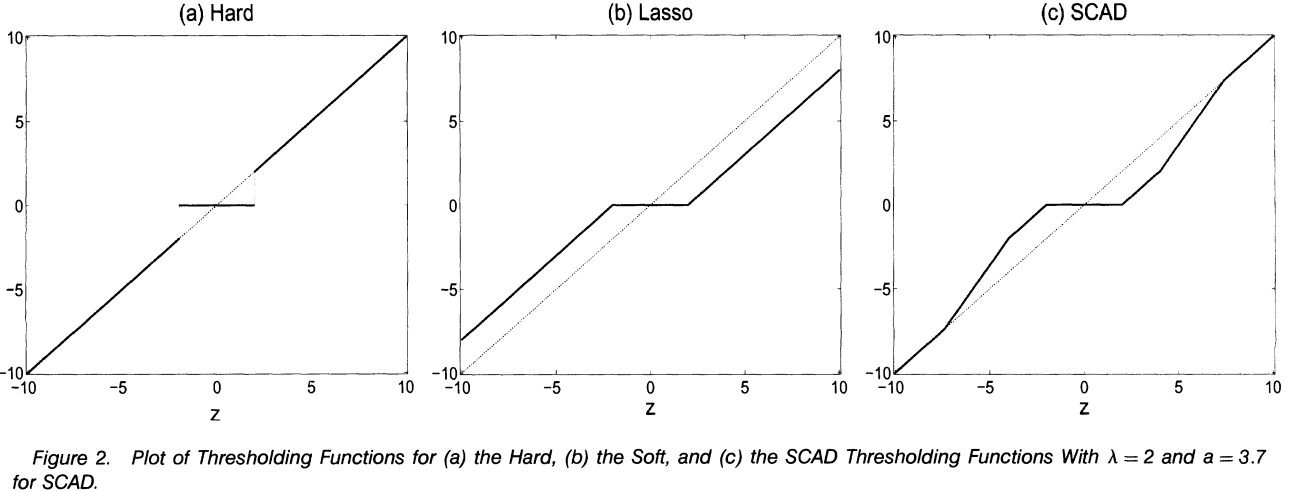
图 16.8: 硬阈值、软阈值和SCAD的解
优点
- 结合了硬阈值和\(L_1\)惩罚的优点,提供了连续且具有阈值特性的解。
- 通过局部二次近似,\(SCAD\)惩罚能够减少大系数的惩罚,同时保持变量选择的特性。
- \(SCAD\)在高信噪比情况下表现良好,能够准确地识别出重要的变量。
缺点
- 需要估计额外的参数,这可能增加计算复杂度。
- \(SCAD\)的计算可能比\(Lasso\)和\(Adaptive \; Lasso\)更复杂,尤其是在处理大量变量时。
16.2.4 Adaptive Lasso
glmnet包的glmnet()函数 orARGOS包的alasso()函数
Hui Zou[17]改进了\(Lasso\)回归,在其文章中提出了\(Adaptive \; Lasso\),能够根据不同系数分配不同的权重,解决了\(Lasso\)变量选择不一致的问题,具有\(Oracle\)性质。
\(Adaptive \; Lasso\)的惩罚函数为
\[ P_{\lambda, w}(\beta)=\lambda\sum_{i=1}^p w_i|\beta_i| \tag{16.13} \]
其中\(w_i\)为权重,可通过数据驱动得到。以\(3|\beta_1|+|\beta_2|\)为例绘制惩罚函数图。
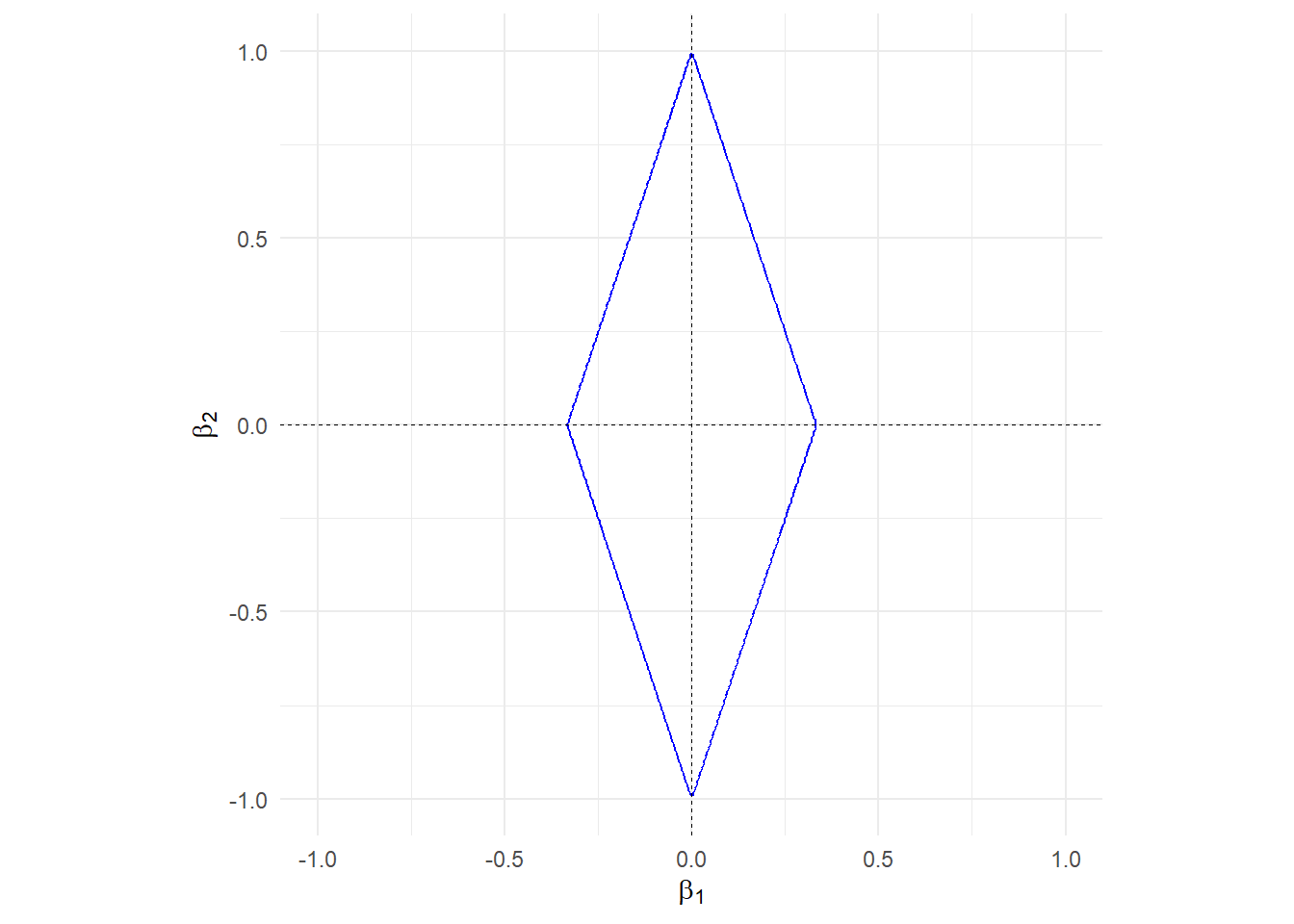
图 16.9: Adaptive Lasso的惩罚函数
\(Adaptive \; Lasso\)的解如图16.10所示,显然满足无偏性、稀疏性和连续性
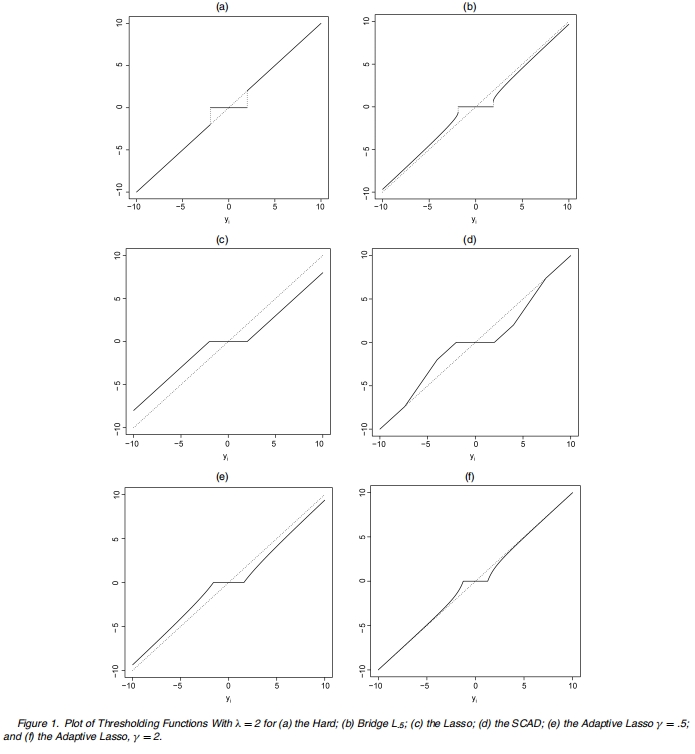
图 16.10: Adaptive Lasso的解
优点
- 通过使用数据依赖的权重对不同的系数进行惩罚,改进了\(Lasso\)方法。
- 具有\(Oracle\)性质。
- 在预测准确性和变量选择上,\(Adaptive \; Lasso\)能够平衡\(Lasso\)和\(SCAD\)的优点。
缺点
- 需要选择合适的正则化参数,这可能需要依赖于数据驱动的方法。
T老师建议,当\(p\)很大时,\(SCAD\)优于\(Adaptive \; Lasso\)。当\(p>>n\)时,选用\(Sure \; Independence \; Screening\)法。