7.3 随机森林

在介绍随机森林前，先介绍装袋法Bagging。

Bagging基于自助采样法bootstrap来抽取多个具有相同样本量的训练集，然后在各个训练集上对基学习器进行训练，最终将这些基学习器结合起来。而对于那些没有被纳入到训练集中的样本，可以作为测试集来计算测试误差，称为袋外误差OOB-error。

结合策略可以是投票法、简单平均法、加权平均法等策略。

随机森林，顾名思义，基于Bagging的方法构建多棵决策树形成森林，其“随机”不仅体现在训练集的随机，还体现在每棵决策树的初始特征也是随机选取的。这使得随机森林相较决策树有更加优秀的泛化能力。

7.3.1 实现

randomForest包是R中专门用来构建随机森林模型的包。下面将详细介绍包中的核心函数randomForest()，并罗列其余函数的作用。

用途

该函数使用Breiman的随机森林算法进行回归与分类任务。
参数
- x
  
  存储预测变量的数据框或矩阵。
- y
  
  响应变量向量。若为因子型变量，则视为分类树，否则视为回归树。若为省略，则为无监督模式。
- xtest
  
  预测变量的测试集，为数据框或矩阵格式。
- ytest
  
  响应变量的测试集，向量格式。
- ntree
  
  决策树的数目，默认为500。
- mtry
  
  随机属性子集的大小。分类任务为属性总量的平方根，回归任务为属性总量三分之一。
- weights
  
  权重向量，在采样时为训练集中的不同观测点设置权重。
- replace
  
  是否为有放回抽样，默认为TRUE。
- classwt
  
  在分类任务中，设置类的先验概率。注意传入的是一个向量，向量的分量表示不同类别的比例，这些分量无须加总为1。
- cutoff
  
  在分类任务中，设置投票法的阈值，即超过多少比例才认为该观测点属于特定的一类。
- strata
  
  一个被用于分层抽样的因子型变量。
- sampsize
  
  样本容量。在分类任务中，若其为与strata相同长度的向量，则表示不同层的样本容量。
- nodesize
  
  表示叶结点位置的最小样本数，默认分类任务为1，回归任务为5。
- maxnodes
  
  表示叶结点的最大个数，若不指定，则决策树将会尽可能地生长。
- importance
  
  是否评估预测变量的重要性，默认为FALSE。
- localImp
  
  是否需要计算重要性度量，默认为FALSE。若为TRUE，则会覆盖掉importance参数。
  
  该参数和importance参数的区别貌似在于前者用于局部重要性度量，后者用于全局重要性度量。
- nPerm
  
  在回归任务中，该参数用于评估变量重要性时对每棵树的袋外数据进行排列的次数。
- proximity
  
  是否计算观测点之间的相似度。
- oob.prox
  
  是否计算袋外数据观测点之间的相似度。
- norm.votes
  
  在分类任务中，若为TRUE，则以比例形式展示最终的投票结果；若为FALSE，则展示原始票数。默认为TRUE。
- do.trace
  
  是否在控制台输出详细的运行过程，默认为FALSE。若为整数，则表示每构建多少棵树就输出一次详情。
- keep.forest
  
  是否在输出结果中保留森林。若给定了xtest，则默认为FALSE。
- corr.bias
  
  在回归任务中，是否对回归结果进行偏差校正。
  
  该参数是实验性的，风险自担。
- keep.inbag
  
  是否返回\(n \times ntree\)矩阵用以记录哪些观测点在哪棵树中被使用。
输出
- call
  
  模型的输入信息。
- type
  
  树的类别，回归任务还是分类任务还是无监督模式。
- predicted
  
  基于袋外样本的预测值。
- importance
  
  重要性度量矩阵，返回所有变量的平均下降精度、平均下降基尼系数或者平均下降MSE。
- importanceSD
  
  重要性度量的标准误矩阵。
- localImp
  
  局部重要性度量矩阵，返回变量对观测点重要性的度量。
- ntree
  
  决策树的数量。
- mtry
  
  每个结点上随机属性子集的大小。
- forest
  
  包含整个森林的列表。当randomForest()处于无监督模式或者keep.forest为FALSE时为NULL值。
- err.rate
  
  在分类任务中，第i棵树及之前所有树在袋外数据中的分类错误率。
- confusion
  
  在分类任务中，分类结果的混淆矩阵。
- votes
  
  在分类任务中，显示得票比例或者得票数。
- oob.times
  
  观测点归为袋外数据的次数。
- proximity
  
  接近度矩阵，根据观测点在同一结点出现的频率来计算观测点之间的相似性。
- mse
  
  回归任务中的均方误差。
- rsq
  
  伪R方，\(1-\frac{mse}{Var(y)}\)
- test
  
  若在输入中给出了测试集的数据，则在结果中会以列表形式存储关于测试集的有关结果。

randomForest包中的其余函数的作用如下表所示。

函数名	用途
classCenter	返回不同类别的原型
combine	将多个森林合并为一个大森林
getTree	从森林中提取一棵决策树
grow	为森林新添决策树
importance	提取变量重要性度量
imports85	一个UCI机器学习数据集
margin	计算或绘制分类边界
MDSplot	绘制接近度矩阵的多维尺度图
na.roughfix	利用中位数或众数来估算缺失值
outlier	根据接近度矩阵计算离群点
partialPlot	绘制偏依赖图
plot.randomForest	绘制随机森林的分类错误率或者MSE
predict.randomForest	用测试集进行预测
treecv	利用交叉验证法进行特征选择
treeImpute	利用接近度矩阵来估算自变量中的缺失值
treeNews	查看randomForest包的更新文件
treesize	查看每棵树的叶结点数或总结点数
tunetree	调优以寻找mtry的最优参数值
varImpPlot	可视化变量的重要性度量
varUsed	查看随机森林实际用到了哪些自变量

下面生成随机数据供随机森林进行模拟。

library(tidyverse)
library(randomForest)
library(MASS)  # 用到多元正态随机数

首先自定义函数，用于生成模拟数据。

# 自定义函数——生成多元正态数据
gen_data <- function(level, size, mu, sigma) {
    # 初始化数据框
    df = data.frame()

    # 生成每个类别的数据
    for (i in 1:level) {
        # 生成类别标签
        category_label = rep(LETTERS[i], size[i])

        # 生成数据
        category_data = as.data.frame(mvrnorm(n = size[i], mu = mu[[i]], Sigma = sigma[[i]]))

        # 添加类别标签
        category_data$category = factor(category_label)

        # 将数据添加到数据框
        df = rbind(df, category_data)
    }

    # 返回数据框
    return(df)
}

# 自定义函数——生成协方差矩阵
gen_sigma <- function(n) {
    # 生成一个n x n的随机矩阵
    L = matrix(runif(n * n, min = 1, max = 2), ncol = n)
    diag(L) = abs(diag(L))  # 确保对角线上的元素为正

    # 填充上三角部分为0
    L[upper.tri(L)] = 0

    # 计算Cholesky分解
    A = L %*% t(L)

    return(A)
}

分类任务

这里生成具有3个水平的响应变量和9个预测变量。注意到不同类别之间的样本量存在一定的差异。

set.seed(123)
mu <- list(runif(9, min = 1, max = 4), runif(9, min = 1, max = 4), runif(9, min = 1,
    max = 4))
sigma <- list(gen_sigma(9), gen_sigma(9), gen_sigma(9))
df_train <- gen_data(level = 3, size = c(100, 300, 600), mu = mu, sigma = sigma)
df_test <- gen_data(level = 3, size = c(30, 100, 180), mu = mu, sigma = sigma)

接着运行模型。

tree_class <- randomForest(x = df_train[, -10], y = df_train$category, importance = T)
print(tree_class)

## 
## Call:
##  randomForest(x = df_train[, -10], y = df_train$category, importance = T) 
##                Type of random forest: classification
##                      Number of trees: 500
## No. of variables tried at each split: 3
## 
##         OOB estimate of  error rate: 16.2%
## Confusion matrix:
##    A   B   C class.error
## A 34  35  31  0.66000000
## B  3 221  76  0.26333333
## C  0  17 583  0.02833333

可以看到，袋外数据的分类错误率为16.2%。其中A类的分类错误率高达66%，这可能和训练集中的类别比例有关。

进一步地，绘制出分类错误率随决策树增加的变化趋势，可以更清晰地看到分类错误率的收敛情况。

plot(tree_class, col=c('black','red','blue','brown'), 
    lty=1, lwd=2, main='OOB err.rate')
legend('topright', legend=colnames(tree_class$err.rate), 
      col=c('black','red','blue','brown'),
      lty=1, lwd=2)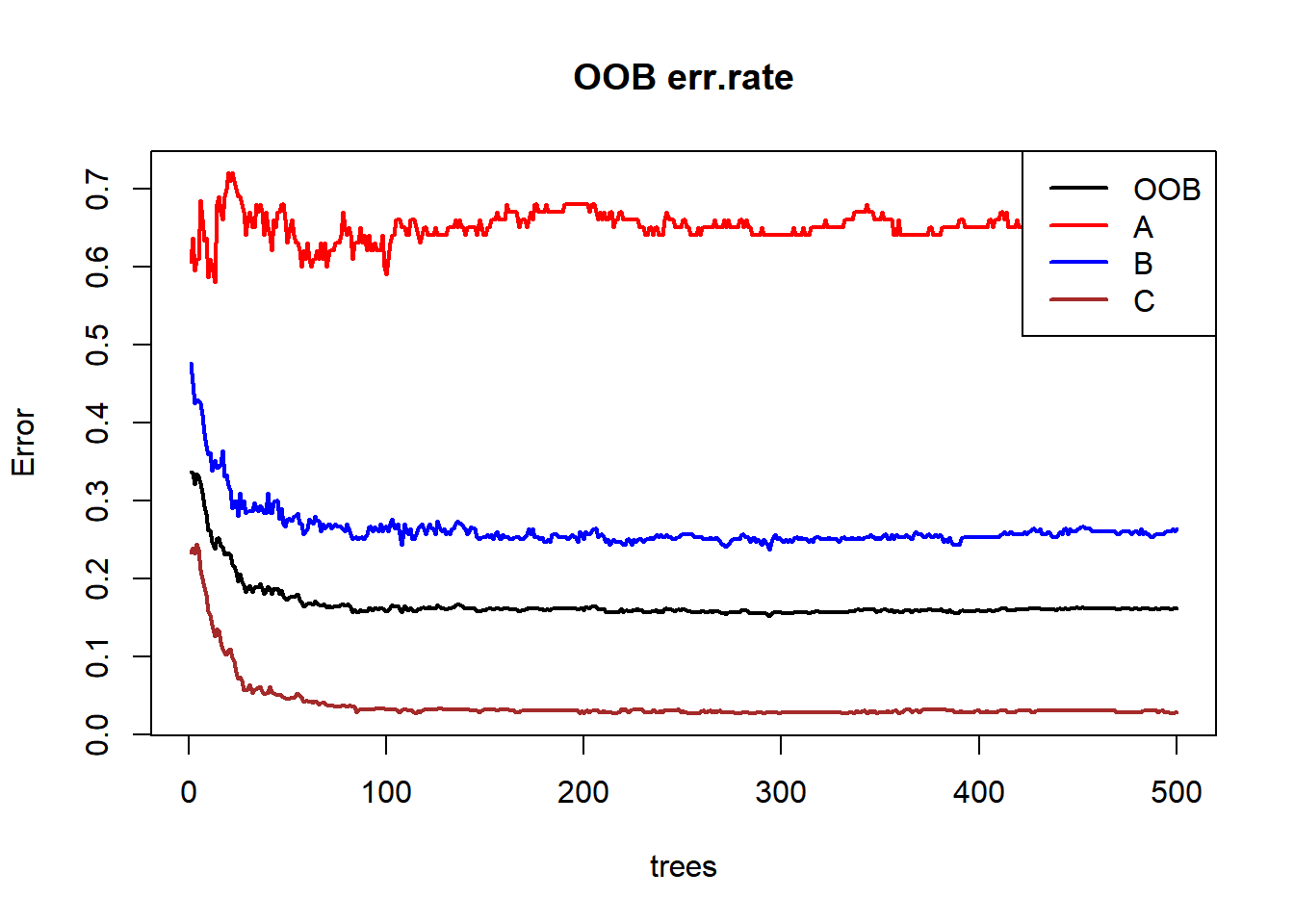

图 7.1: 袋外数据的分类错误率

再来看看不同特征的重要程度。对于一棵树，在随机打乱某个特征的值的顺序之后，可以作差得到前后预测精度的下降情况，对于所有树取平均即可得到平均下降精度(MDA)。显然，如果MDA越大，说明该特征就越重要。同理，平均下降基尼系数(MDI)通过计算每个特征在所有树上节点分裂时导致的基尼系数平均下降量来评估特征的重要性。基尼系数反映了不纯度，下降得越多说明结点越容易从“不纯”走向了“纯”，意味着该特征在区分不同类别时能够较为显著地发挥作用。由图可知，两种评价准则得到的结果较为一致。

varImpPlot(tree_class)

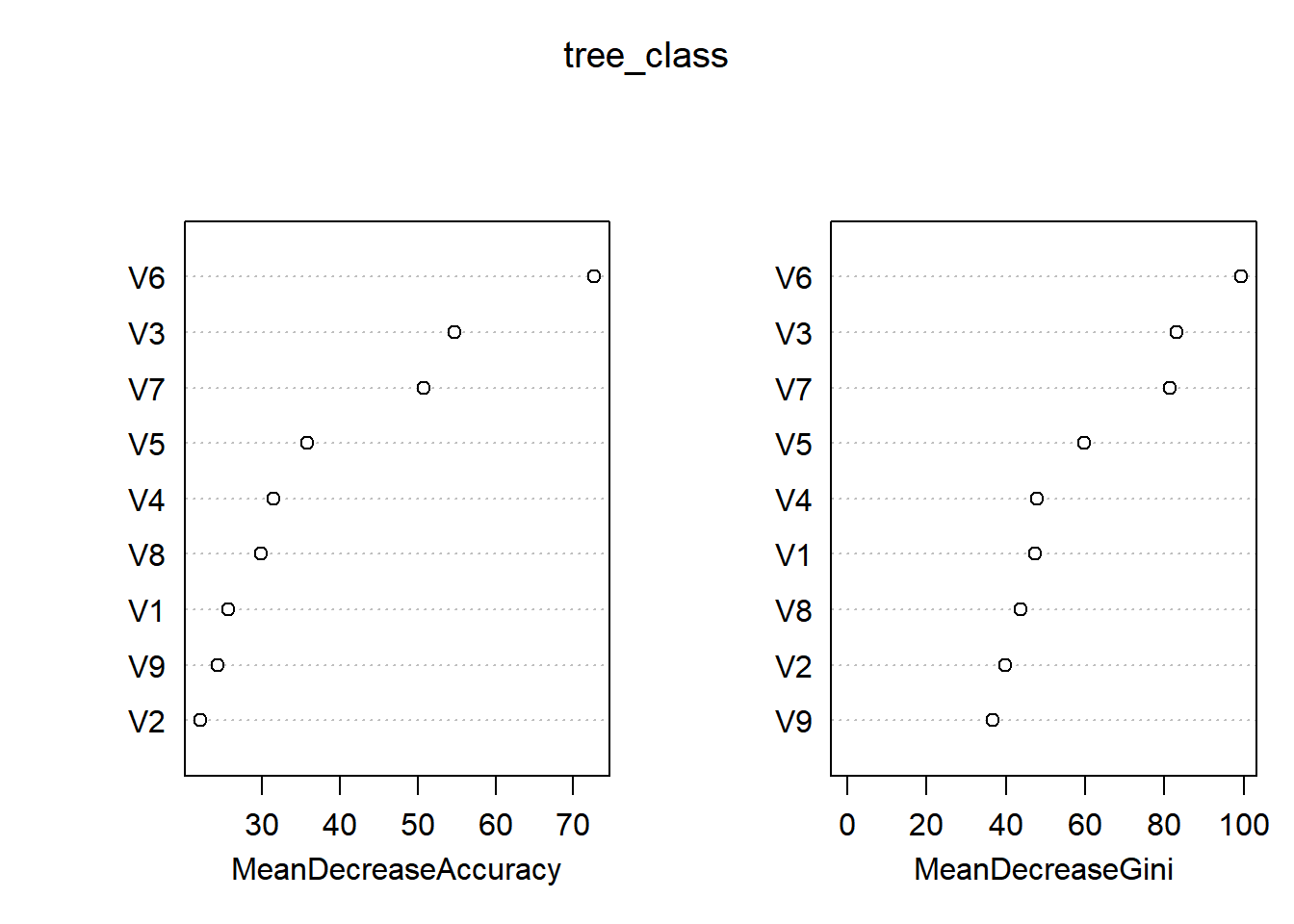
图 7.2: 分类_重要性度量

下面关注如何缓解类不平衡问题及如何选取最优参数mtry。

注意到训练集中类别的比例为1:3:6，存在一定程度的类不平衡问题。对此，在运行随机森林模型时可以设置classwt参数来设定各个类别的先验概率。

tree_class_prior <- randomForest(x = df_train[, -10], y = df_train$category, importance = T,
    proximity = T, classwt = c(1, 3, 6))
print(tree_class_prior)

## 
## Call:
##  randomForest(x = df_train[, -10], y = df_train$category, classwt = c(1,      3, 6), importance = T, proximity = T) 
##                Type of random forest: classification
##                      Number of trees: 500
## No. of variables tried at each split: 3
## 
##         OOB estimate of  error rate: 15.8%
## Confusion matrix:
##    A   B   C class.error
## A 32  37  31        0.68
## B  5 228  67        0.24
## C  0  18 582        0.03

而对于参数mtry的选取，除了可以使用randomForest包自带的tunetree()函数进行调参，还可以自己写个循环，直接根据测试集来选取最优参数。

err.rate <- c(1:9)
for (i in 1:9) {
    tree = randomForest(x = df_train[, -10], y = df_train$category, mtry = i)
    fit_test = predict(tree, df_test[, -10])
    err.rate[i] <- sum(fit_test != df_test$category)/nrow(df_test)
}
plot(1:9, err.rate, type = "b", lwd = 2, xlab = "mtry", ylab = "test err.rate")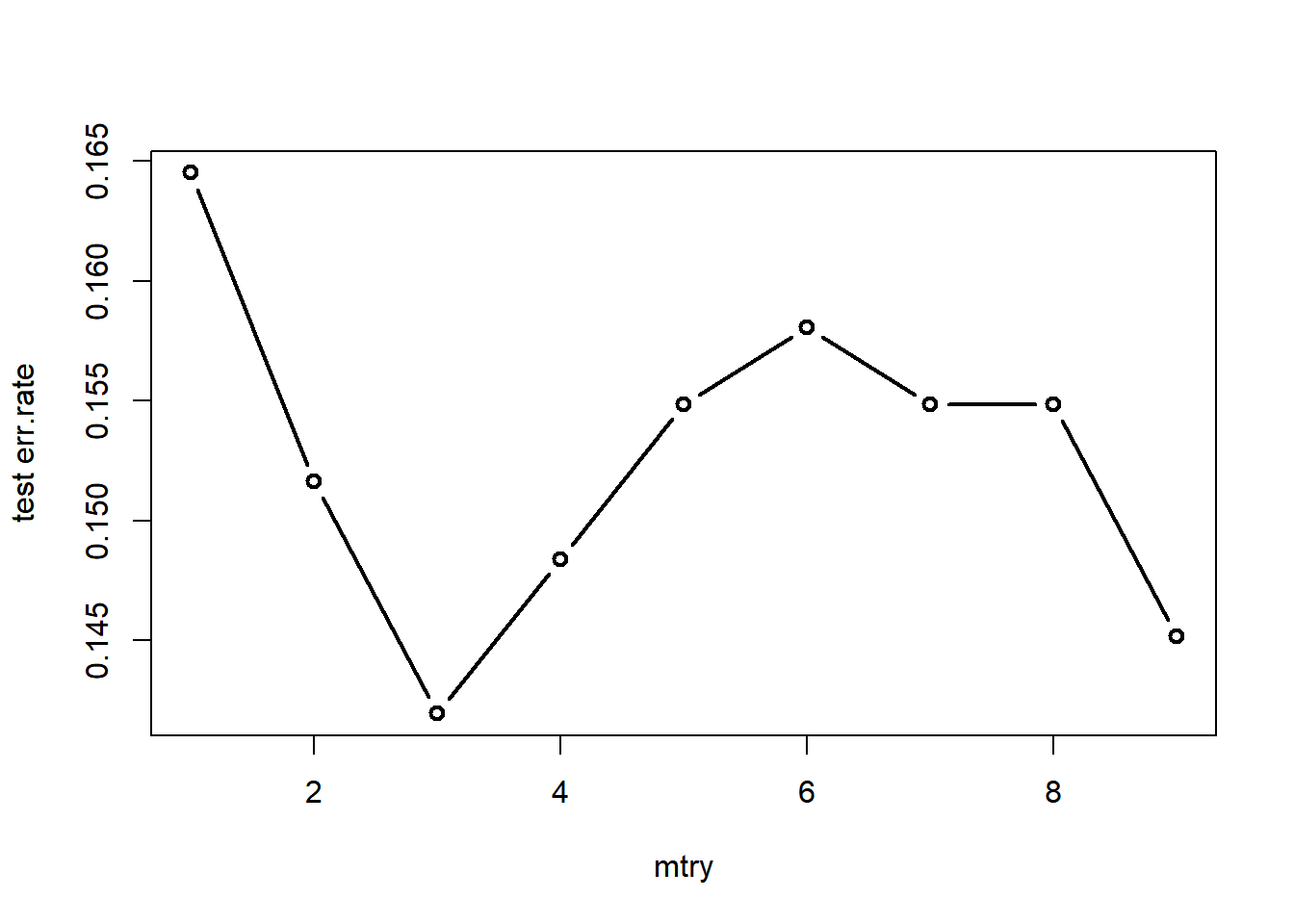

图 7.3: 分类_mtry调优

由图可知，当mtry=3时，在测试集上的袋外数据分类错误率达到最小，为14.2%。

回归任务

这里首先生成自变量数据，然后在自变量的线性组合的基础上添加噪声，得到因变量数据。

set.seed(111)
mu <- list(runif(9, min = 1, max = 4))
sigma <- list(gen_sigma(9))
df_train <- gen_data(level = 1, size = c(1000), mu = mu, sigma = sigma)
df_train$epsilon <- rnorm(1000, sd = 3)
df_train <- df_train %>%
    mutate(y = 2 * V1 + 3 * V2 + V3 + 4 * V4 + 3 * V5 + V6 + 2 * V7 + 3 * V8 + 4 *
        V9 + epsilon)

df_test <- gen_data(level = 1, size = c(100), mu = mu, sigma = sigma)
df_test$epsilon <- rnorm(100, sd = 3)
df_test <- df_test %>%
    mutate(y = 2 * V1 + 3 * V2 + V3 + 4 * V4 + 3 * V5 + V6 + 2 * V7 + 3 * V8 + 4 *
        V9 + epsilon)

接着直接运行模型。

tree_reg <- randomForest(x = df_train[, 1:9], y = df_train$y, importance = T)
print(tree_reg)

## 
## Call:
##  randomForest(x = df_train[, 1:9], y = df_train$y, importance = T) 
##                Type of random forest: regression
##                      Number of trees: 500
## No. of variables tried at each split: 3
## 
##           Mean of squared residuals: 46.75519
##                     % Var explained: 98.91

从结果中可以看到，均方误差为46.7551872，自变量能解释的变异程度为98.91%。

进一步地，下面给出了模型的袋外数据MSE。

plot(tree_reg, main='OOB mse', lwd=2)

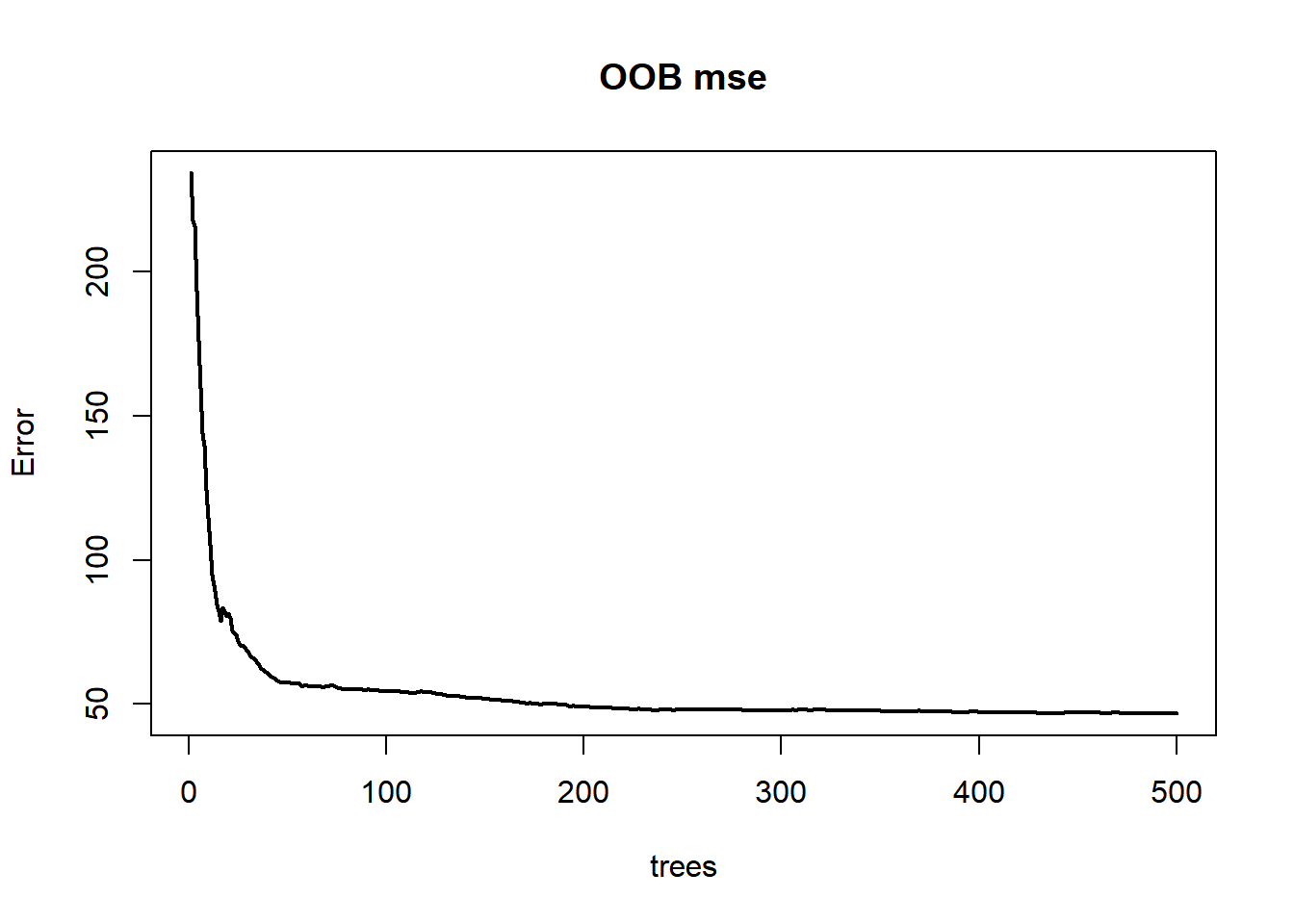
图 7.4: 袋外数据MSE

再来看看特征的重要性度量。其中%IncMSE表示重排某个特征前后袋外数据MSE的上升百分比，上升的幅度越大，说明该特征对模型更加重要。IncNodePurity则表示结点分列时残差平方和的下降情况。

varImpPlot(tree_reg)

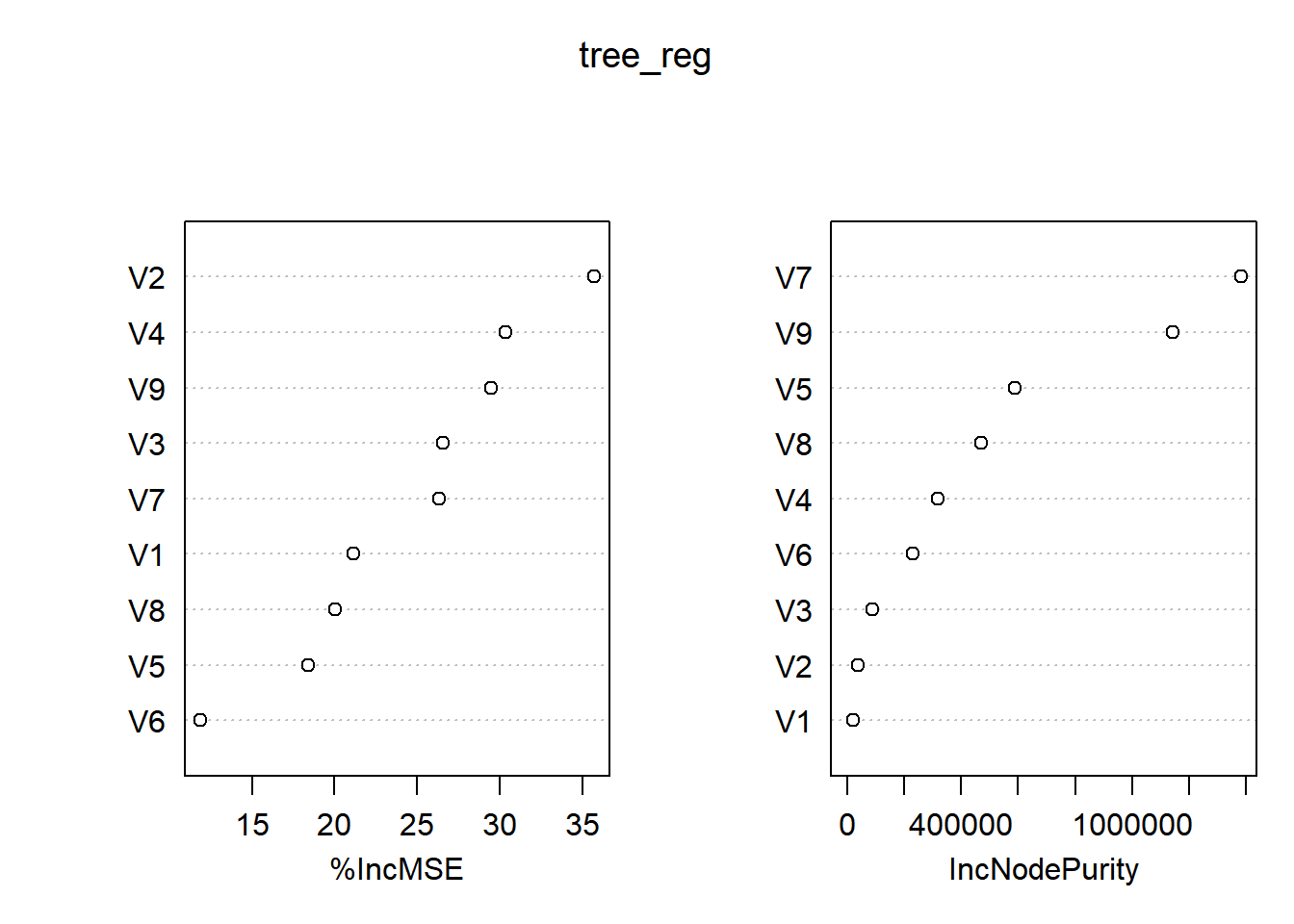
图 7.5: 回归_重要性度量

最后，给模型参数mtry调调优。

mse <- c(1:9)
for (i in 1:9) {
    tree = randomForest(x = df_train[, 1:9], y = df_train$y, mtry = i)
    fit_test = predict(tree, df_test[, 1:9])
    mse[i] <- sum((fit_test - df_test$y)^2)/nrow(df_test)
}
plot(1:9, mse, type = "b", lwd = 2, xlab = "mtry", ylab = "test MSE")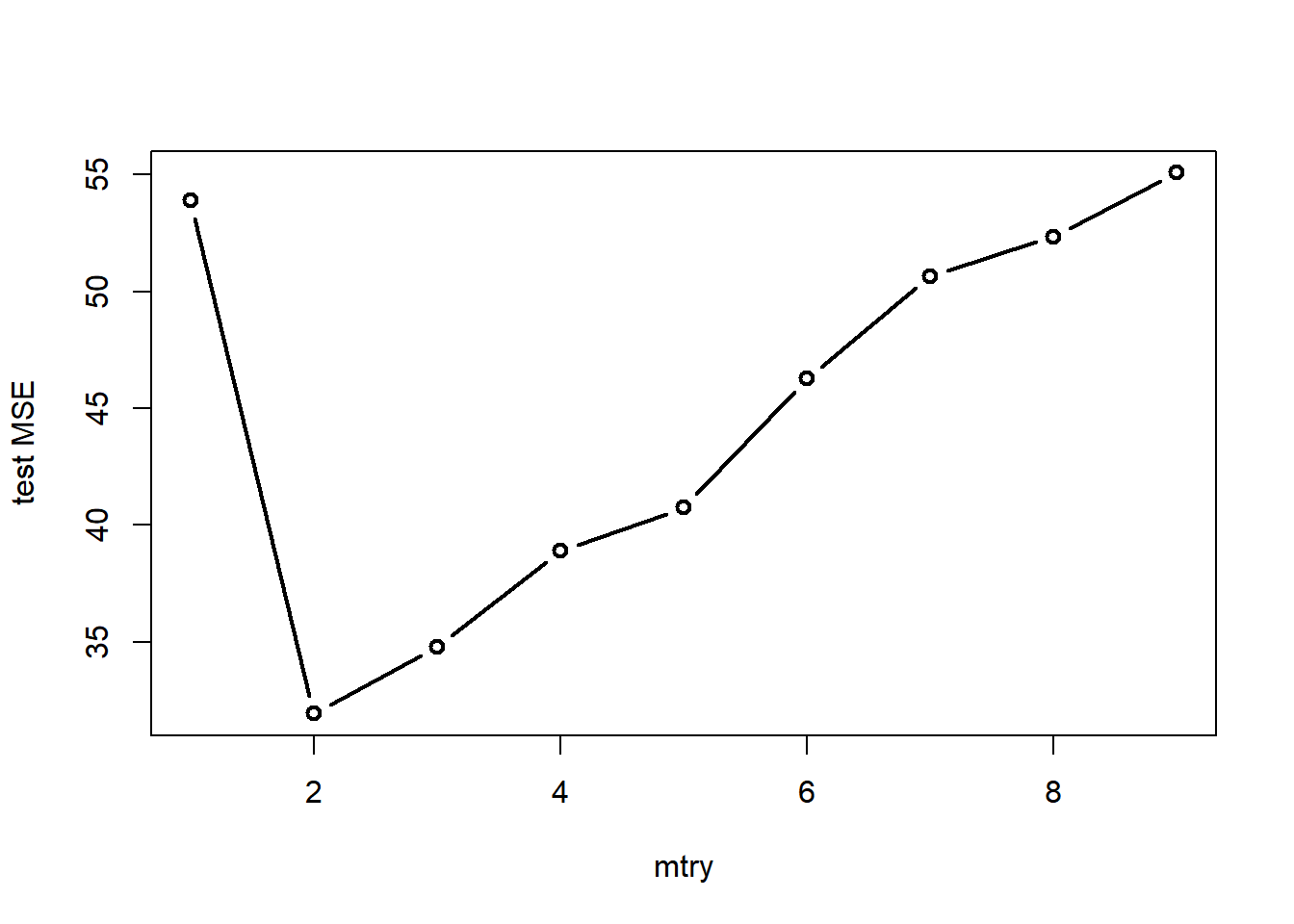

图 7.6: 回归_mtry调优

由图可知，当mtry=2时，在测试集上的袋外数据MSE达到最小，为31.9。