10.6 Seq2Seq

10.6.1 原理

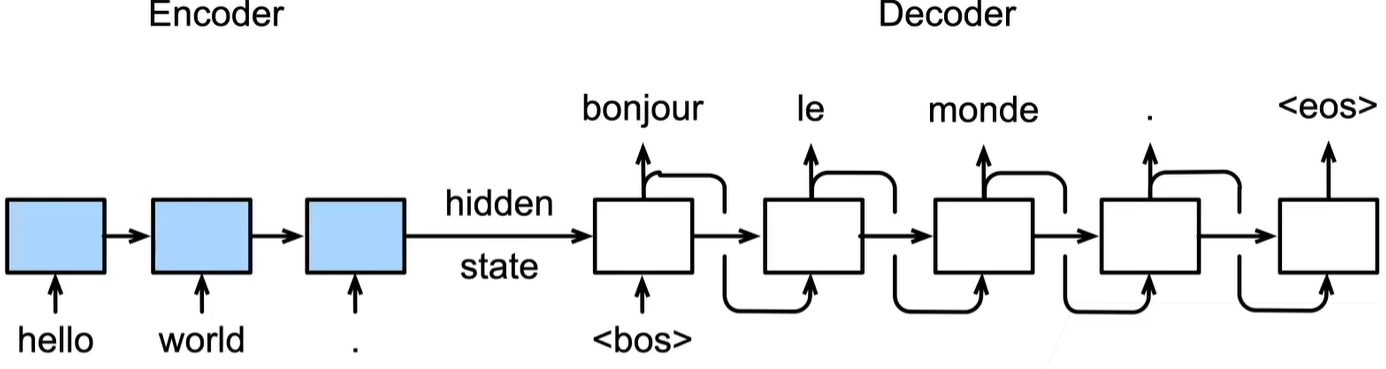
seq2seq

图 10.4: seq2seq

当然对于翻译任务，应当有个词嵌入环节

Seq2Seq由编码器和解码器组成，二者均是RNN（包括LSTM和GRU）结构，用于解决由原始序列输出目标序列的任务，两个序列可以不等长。

在编码器部分，由于输入序列已知，因此可以使用双向RNN结构用于提取信息，然后在最后一个时间步输出隐状态，并将此隐状态作为上下文向量context vector，记为\(c\)。

上下文向量相当于是对原始序列信息的一个浓缩

在解码器部分，若记解码器的隐状态为\(s\)，则

\[ s_t = f(s_{t-1}, y_{t-1}, c) \]

即解码器t时刻的隐状态由上一步的隐状态、上一步的预测值、编码器的上下文向量共同输入得到。

在训练时，采取\(Teacher Forcing\)策略，即每次输入的\(y\)值为真实值，这有助于模型训练。但在预测时则接收上一步的预测值作为输入

但是，Seq2Seq有很明显的缺陷，即在解码器中使用的上下文向量是固定的，而由于编码器的RNN结构，导致这个上下文向量难以记住更早的重要信息。于是，提出Seq2Seq+注意力机制的方法。

下面介绍Luong的论文Effective Approaches to Attention-based Neural Machine Translation。

这篇论文可以说是对Bahdanau的NEURAL MACHINE TRANSLATION BY JOINTLY LEARNING TO ALIGN AND TRANSLATE这篇论文的改进，有细微差异，例如这篇论文用\(s_{t-1}\)来更新\(c_t\)，而Luong用\(s_t\)

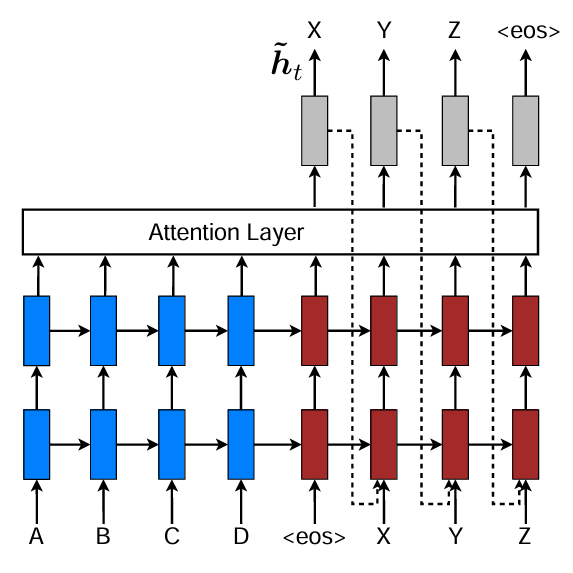
Seq2Seq与注意力机制（Input-Feeding）

图 10.5: Seq2Seq与注意力机制（Input-Feeding）

计算流程为：

  1. 编码阶段

输入序列 \((x_1, x_2, \ldots, x_S)\) 经双向LSTM编码得到：

\[ h_1, h_2, \ldots, h_S = \text{EncoderRNN}(x_1, \ldots, x_S) \]

每个\(h_s\)是源序列中第\(s\)个词的隐状态输出。

  1. 解码器状态更新

在时间步\(t\)，解码器根据上一步输出的目标词\(y_{t-1}\)与前一隐藏状态 \(s_{t-1}\)，更新当前解码器状态：

\[ s_t = \text{DecoderRNN}(y_{t-1}, s_{t-1}) \]

此时 \(s_t\) 表示“当前要生成第 \(t\) 个词”的语义状态。

论文还提出了Input-Feeding机制，即在生成\(s_t\)时也用到了\(\tilde{s}_{t-1}\)的信息，\(\tilde{s}_{t-1}\)后续会介绍。

\[ s_t = \text{DecoderRNN}(y_{t-1}, \tilde{s}_{t-1}, s_{t-1}) \]

  1. 注意力机制

通过相似度函数计算\(s_t\)与每个\(h_s\)的匹配程度，论文中介绍了三种计算方法：

\[ \text{score}(s_t, h_s) = \begin{cases} s_t^\top h_s, & \text{(Dot)} \\ s_t^\top W_a h_s, & \text{(General)} \\ v_a^\top \tanh(W_a [s_t; h_s]), & \text{(Concat)} \end{cases} \]

Bahdanau的论文中使用\(e_{t,i}= v_a^{T} \text{tanh}(W_ss_{t-1}+W_hh_i)\)加性注意力函数来计算相似度得分

之后通过softmax归一化得到每个源词的注意力权重：

\[ a_t(s) = \frac{\exp(\text{score}(s_t, h_s))} {\sum_{s'=1}^{S} \exp(\text{score}(s_t, h_{s'}))} \]

其中\(a_t(s)\) 表示当前解码器在生成第\(t\)个词时，关注源序列\(s\)个位置的程度。

  1. 计算上下文向量

对编码器输出进行加权求和，得到上下文向量：

\[ c_t = \sum_{s=1}^{S} a_t(s)\, h_s \]

\(c_t\)是源端信息的加权摘要，代表模型在第\(t\)步“看到”的输入信息。

  1. 信息融合

Luong 定义了attentional hidden state：

\[ \tilde{s}_t = \tanh(W_c [c_t; s_t]) \]

该向量综合了当前目标语义与注意到的源端信息。

  1. 输出词预测

通过线性层与 softmax 计算目标词概率分布：

\[ p(y_t \mid y_{<t}, x) = \text{softmax}(W_o \tilde{s}_t) \]

取概率最大的词作为预测输出：

\[ \hat{y}_t = \arg\max_y p(y_t) \]