10.10 Transformer
10.10.1 原理
在Transformer之前,自然语言处理的主流方法是RNN等循环神经网络,存在
序列依赖强 → 无法并行训练
长距离依赖弱 → 远距离词之间信息传递困难
训练慢 → 不适合大规模语料
等问题。而Transformer完全使用注意力机制来处理序列,从而解决了这些问题。
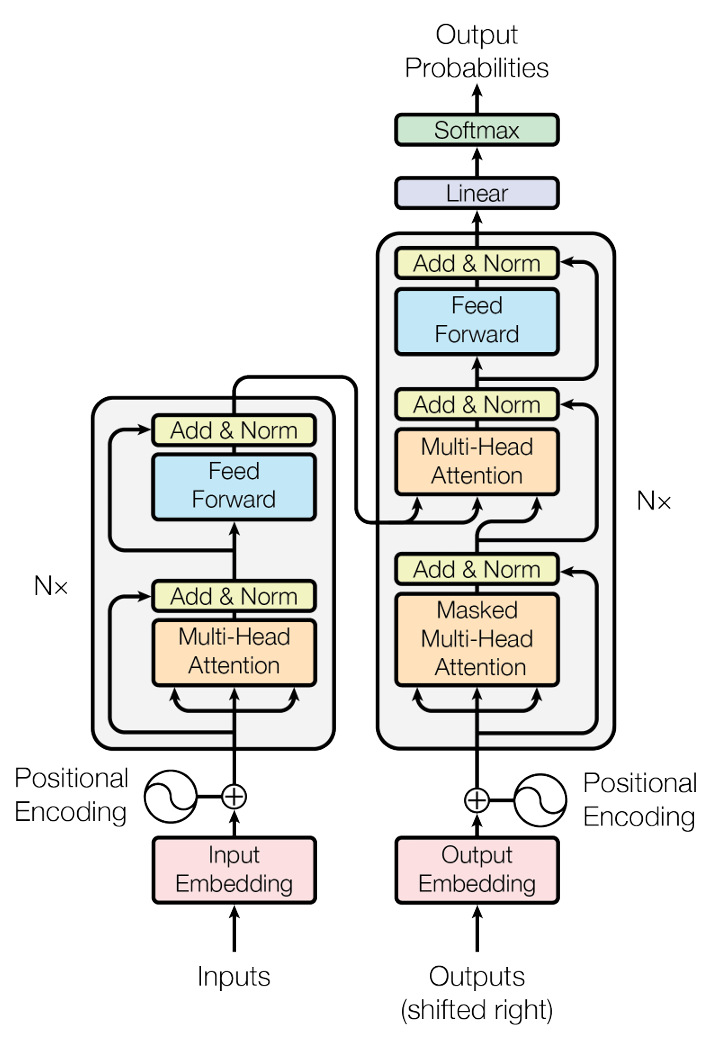
图 10.6: Transformer
10.10.1.1 整体结构
Transformer采用编码器-解码器架构。
原始论文中采用6层编码器和6层解码器
- 编码器
多头注意力机制
前馈神经网络
残差连接+层归一化
- 解码器
掩码多头自注意力机制
多头自注意力机制
前馈神经网络
残差连接+层归一化
10.10.1.2 注意力机制
- 自注意力机制
\[ \begin{gather} Q = XW_Q, \quad K = XW_K, \quad V=XW_V \\ \text{Attention}(Q,K,V) = \text{softmax}(\frac{QK^T}{\sqrt{d_k}})V \end{gather} \]
自注意力机制中,Q,K,V都是由X线性变换得到。
Q,K,V,X的每一行都是一个词的词向量
Q:Query,当前位置元素的查询请求
K:Key,其他词提供什么样的信息,用于计算与Q的相似度
V:Value,最终实际提供的信息内容
也就是说,\(QK^T\)是为了计算Query向量与Key向量之间的相似度,并通过softmax进行归一化,从而得到权重矩阵(行和为1),与V相乘得到差异化的信息(而不是对每个位置一视同仁)。
\(QK^T\)的点积结果与维度相关,除以\(d_k\)可将方差控制为1,有效避免因数值较大导致softmax过度关注某个位置而忽略其他位置
- 多头注意力机制
而多头注意力机制则是多个自注意力机制的叠加。
\[ \begin{gather} \text{head}_i = \text{Attention}(Q_i, K_i, V_i) \\ \text{MultiHead}(Q,K,V) = \text{Concat}(\text{head}_1, \dots, \text{head}_h)W^O \end{gather} \]
将每个自注意力机制的输出拼接在一起,再通过\(W^O\)重新映射回与X相同的维度。
- 掩码注意力机制
在解码器部分,当捕捉序列的上下文信息时,我们是没法看到当前元素之后的其他元素信息,因此在计算注意力得分前需要构造Mask矩阵来掩盖当前元素之后的元素仅在当前元素及之前元素上计算注意力得分。
- 交叉注意力机制
在解码器部分,为了获取编码器输出的上下文信息,交叉注意力机制中设置Q为解码器第一个注意力机制的输出,而K和V都设置为编码器输出的隐状态向量,这样就能获取到与当前序列相关的编码器部分的上下文信息。
10.10.1.3 位置编码
Transformer不像RNN等循环神经网络那样,能够自然而然的体现出先后顺序。为了捕捉元素的先后顺序关系,Transformer采用位置编码来提取位置信息。
\[ PE_{pos,2i} = \sin{(\frac{pos}{10000^{2i/d}})} \\ PE_{pos,2i+1} = \cos{(\frac{pos}{10000^{2i/d}})} \]
对于第pos位置的元素,其位置编码为交替的sin和cos函数值,并且维度分为两两一对,每对中的频率是一样的
这样设置能够在较低维度(频率高变化快)捕捉局部位置信息,在较高维度(频率低变化慢)捕捉全局位置信息。
此外,根据正弦函数的性质,\(PE_{pos+k}\)能够表示为\(PE_{pos}\)的线性函数,也就是能够表示相对位置关系。