9.9 聚类分析
9.9.1 聚类结果评价
轮廓系数
轮廓系数综合考虑了样本在自身簇内的紧密程度和与其他簇的分离程度。
\[ a(i) = \frac{1}{|C_i| - 1} \sum_{j \in C_i, j \neq i} d(i, j) \]
\[ b(i) = \min_{k \neq i} \frac{1}{|C_k|} \sum_{j \in C_k} d(i, j) \]
其中: - \(a(i)\):样本 \(i\) 到同簇中其他样本的平均距离; - \(b(i)\):样本 \(i\) 到最近其他簇的平均距离。
轮廓系数定义为:
\[ s(i) = \frac{b(i) - a(i)}{\max(a(i), b(i))} \]
整体平均轮廓系数:
\[ S = \frac{1}{N} \sum_{i=1}^{N} s(i) \]
取值范围: \([-1, 1]\),越接近 1 表示聚类效果越好。
CH指数
CH指数衡量类间方差与类内方差的比值,类似于方差分析(ANOVA)中的 F 统计量。
设共有\(N\)个样本、\(K\)个簇,第\(k\)个簇的样本数为\(n_k\),簇中心为\(c_k\),全局中心为\(c\)。
定义:
\[ B_k = n_k \| c_k - c \|^2 \]
\[ W_k = \sum_{x_i \in C_k} \| x_i - c_k \|^2 \]
则CH指数为:
\[ CH = \frac{\text{Tr}(B)}{\text{Tr}(W)} \times \frac{N - K}{K - 1} \]
其中:
\[ \text{Tr}(B) = \sum_{k=1}^{K} B_k, \quad \text{Tr}(W) = \sum_{k=1}^{K} W_k \]
取值方向: 越大越好,表示类间分离更明显、类内更加紧密。
Dunn指数
Dunn指数衡量聚类结果的“最差情况”,即最小簇间距离与最大簇内直径的比值。
定义:
\[ \delta(C_i, C_j) = \min_{x \in C_i, y \in C_j} d(x, y) \]
\[ \Delta(C_k) = \max_{x, y \in C_k} d(x, y) \]
Dunn 指数为:
\[ D = \frac{\min_{i \neq j} \delta(C_i, C_j)}{\max_{k} \Delta(C_k)} \]
取值方向: 越大越好,表示簇间更远、簇内更紧密。
但对噪声较敏感。
9.9.2 Kmeans
Kmeans是一种基于距离的划分式聚类算法。其目标是将样本划分为\(K\)个簇,使得同一簇内的样本尽可能相似,不同簇之间的样本尽可能不同。
算法流程:
随机选择\(K\)个样本作为初始中心
对每个样本\(x_i\),计算其到各中心的距离:
\[ \text{assign } x_i \text{ to } C_k \text{ if } \|x_i - \mu_k\|^2 \le \|x_i - \mu_j\|^2, \forall j \]
- 对每个簇\(C_k\)更新中心
\[ \mu_k = \frac{1}{|C_k|}\sum_{x_i \in C_k}x_i \]
- 重复迭代步骤2、3,直至簇分配不再变化或达到最大迭代次数
对初始中心敏感,容易陷入局部最优
需要指定K
只能处理凸形簇
如何确定参数K?
手肘法。计算不同K值下的簇内误差平方和
随着K增大,SSE会逐渐减小,但减小速度在某点后变缓。该“拐点”即为最佳K值。
\[ \text{SSE}(K)=\sum_{k=1}^{K}\sum_{x_i \in C_k}\|x_i-\mu_k\|^2 \]
轮廓系数法
\(a_i\)表示样本与同簇内其他点的平均距离,\(b_i\)表示样本与最近邻簇中所有点的平均距离。轮廓系数\(S\)越大表示聚类效果越好。
\[ \begin{gather} s_i = \frac{b_i - a_i}{\max(a_i, b_i)} \\ S = \frac{1}{n}\sum_{i=1}^{n}s_i, \quad S \in [-1,1] \end{gather} \]
9.9.3 Kmeans++
Kmeans的核心问题在于——对初始簇中心的选择非常敏感:
若初始中心选得不好,算法可能陷入局部最优;
聚类结果依赖随机性,稳定性差;
可能导致“簇塌缩”(多个中心聚到同一区域)。
因此Kmeans++让初始中心尽可能远离彼此,从而覆盖数据空间的主要区域。
算法流程:
- 给定数据集\(X = \{x_1, x_2, \ldots, x_n\}\),以及目标簇数\(K\),随机选择第一个中心:
\[ \mu_1 = x_i, \quad x_i \text{ 从 } X \text{ 中随机选取} \]
- 计算每个点到已有最近中心的距离平方,当前已有中心集合为\(\{\mu_1, \ldots, \mu_m\}\)。
\[ D(x_i)^2 = \min_{1 \le j \le m} \|x_i - \mu_j\|^2 \]
- 按距离加权概率选择下一个中心,距离当前中心越远的点被选为新中心的概率越大。
\[ P(x_i) = \frac{D(x_i)^2}{\sum_j D(x_j)^2} \]
重复步骤2、3,直到选出K个中心。
之后就开始正常的kmeans迭代。
9.9.4 DBSCAN
DBSCAN是一种基于密度的聚类算法,能够在任意形状的数据分布中识别出高密度区域,并自动识别噪声点。
DBSCAN有两个参数:邻域半径\(\varepsilon\)(定义多远的距离算作邻居)与最小样本数minPts(邻域内至少多少个点才算稠密)。
\(\varepsilon\)-邻域定义为
\[ N_\varepsilon(x_i) = \{x_j \mid \text{dist}(x_i, x_j) \le \varepsilon\} \]
| 点类型 | 条件 | 含义 |
|---|---|---|
| 核心点(Core Point) | \(|N_\varepsilon(x_i)| \ge \text{minPts}\) | 位于高密度区域 |
| 边界点(Border Point) | \(|N_\varepsilon(x_i)| < \text{minPts}\),但与核心点相邻 | 位于簇的边缘 |
| 噪声点(Noise Point) | 不属于任何核心点的邻域 | 离群样本 |
直接密度可达:
若\(x_j \in N_\varepsilon(x_i)\),且\(x_i\)是核心点,则\(x_j\)对\(x_i\)直接密度可达。
圆心的影响力
密度可达:
若存在一系列核心点\(x_1, x_2, ..., x_n\),其中\(x_{i+1}\)对\(x_i\)直接密度可达,则\(x_n\)对\(x_1\)密度可达。
圆心相连
密度相连:
若存在核心点\(x_k\),使得\(x_i, x_j\)都密度可达于\(x_k\),则 \(x_i\)与\(x_j\)密度相连。
圆的并集内都是密度相连的
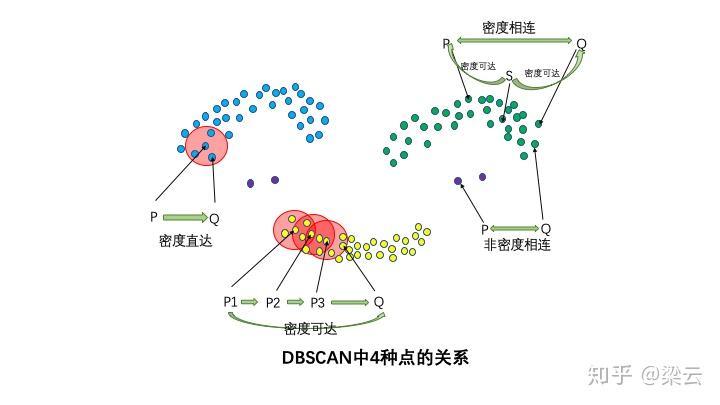
图 9.7: 密度
算法流程:
根据\(\varepsilon\)和minPts找到样本中所有的核心点。
随机取一个核心点,在其邻域中找到所有密度可达点,在从这些密度可达点出发不断拓展,直至拓展后的邻域中再无密度可达点。将这些密度可达点及其邻域内的点归为一个簇。
从剩下的尚未归类的核心点中重新抽取一个核心点,重复步骤2.
当所有核心点已归类时,尚未归类的样本点记为噪声点。
DBSCAN如何调参:
绘制K-距离图:
对每个点计算到第minPts个最近邻的距离;
将这些距离排序并绘制曲线;
曲线的“拐点”即为较优的\(\varepsilon\)值。
2️. 经验规则:
minPts ≈ 2 × 数据维度;
二维数据常取 4~6,高维数据取 10~20。
9.9.5 HDBSCAN
HDBSCAN是一种基于密度的层次聚类算法,是DBSCAN的改进版本。它通过构建多尺度密度层次结构自动识别不同密度的簇并剔除噪声点,从而克服了DBSCAN需要固定\(\varepsilon\)参数、难以处理不同密度区域的缺陷。
传统DBSCAN存在两大局限:
需要手动设定 ε(邻域半径):不同密度簇无法用同一\(\varepsilon\)表示。
无法发现不同密度的簇:固定半径会导致稠密区域被过分细分,稀疏区域被忽略。
HDBSCAN 的核心改进思路是:
不固定\(\varepsilon\),而是从所有可能的\(\varepsilon\)值构建层次结构,
然后通过分析“簇的稳定性”自动剪枝,选出最稳定的聚类结果。
算法流程:
计算核心距离(Core Distance)
对每个点\(x_i\),计算其到第
min_samples个最近邻的距离:
\[ \text{core}_k(x_i) = \text{distance to the } k\text{-th nearest neighbor of } x_i \]
- 计算互相可达距离(Mutual Reachability Distance)
对任意两点\(a, b\)定义:
\[ d_{\text{reach}}(a,b) = \max\{\text{core}_k(a), \text{core}_k(b), d(a,b)\} \] 这样可以防止高密度点“误连接”低密度簇。
构建最小生成树MST
以互相可达距离为边权构造最小生成树(Minimum Spanning Tree)。
构建层次聚类树(Condensed Cluster Tree)
逐步增加距离阈值,相当于逐层“切割” MST,每当一条边被移除,一个簇可能分裂成多个子簇,形成一棵密度树。
计算簇稳定性
对每个簇,计算其在不同密度尺度下的持续时间(即“生存时间”):
\[ \text{stability}(C) = \sum_{x_i \in C} (\lambda_{\text{death}} - \lambda_{\text{birth}}) \]
其中\(\lambda = 1/\varepsilon\),表示密度水平。
提取最稳定簇
根据簇的稳定性评分,剪枝层次树并输出最稳定的聚类结构。
| 参数 | 含义 | 作用 |
|---|---|---|
min_cluster_size |
最小簇大小 | 控制簇的最小规模 |
min_samples |
最小样本数 | 控制密度估计的平滑度(可近似为 DBSCAN 的 minPts) |
metric |
距离度量 | 默认为欧氏距离,可改为曼哈顿、余弦等 |
cluster_selection_method |
簇选择方式 | "eom"(Excess of Mass)或 "leaf"(选择层次树的叶节点) |