10.3 RNN
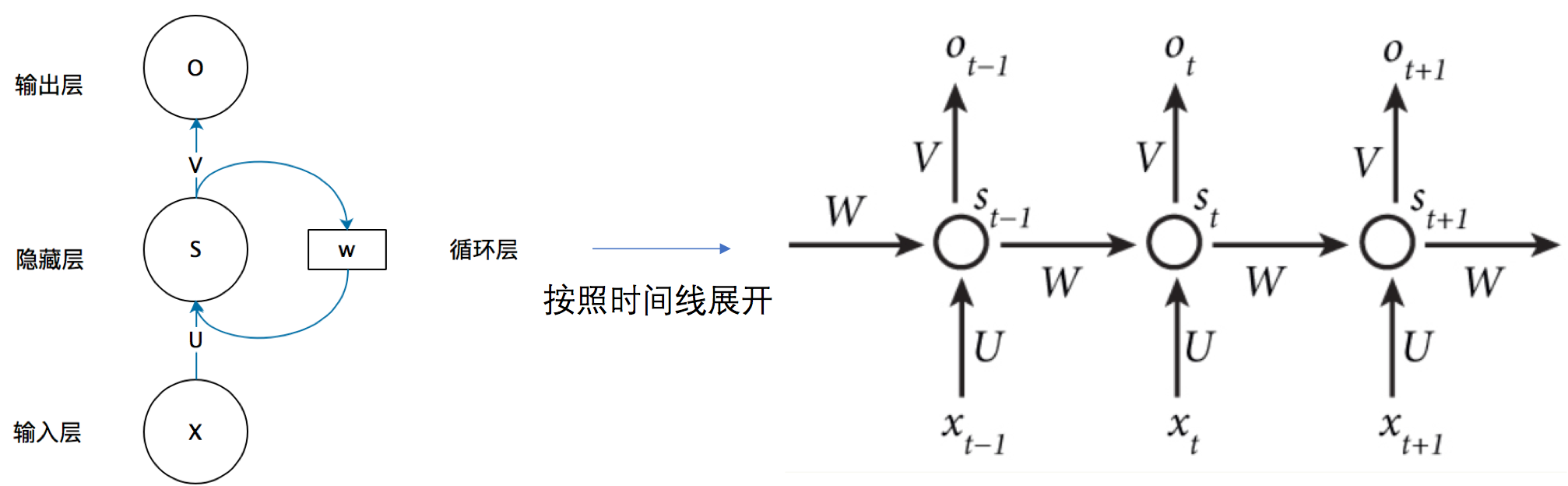
图 10.1: RNN
简单来说,RNN将隐状态在时间上依次传递,当前时间步的隐状态由当前时间步的输入与上一时间步的隐状态得到,当前时间步的输出由当前时间步的隐状态得到。
\[ \begin{gather} s_t = f(W_s s_{t-1} + W_x x_t) \\ o_t = g(W_os_t) \end{gather} \]
但是在训练过程中,由于这种循环结构,容易导致梯度爆炸或消失问题。
对于一个简单的循环神经网络 (RNN),隐藏状态的更新为:
\[ s_t = f(W_s s_{t-1} + W_x x_t) \]
训练RNN时,需要对损失函数\(L_T\)关于参数\(W_s\)求导。
梯度在时间维度上通过链式法则传播:
\[ \frac{\partial L_T}{\partial W_s} = \sum_{t=1}^{T} \frac{\partial L_T}{\partial s_t} \frac{\partial s_t}{\partial W_s} \]
关键项为梯度在时间维上的传播:
\[ \frac{\partial L_T}{\partial s_t} = \frac{\partial L_T}{\partial s_T} \prod_{k=t+1}^{T} \frac{\partial s_k}{\partial s_{k-1}} \]
而每一步的梯度传递因子为:
\[ \frac{\partial s_k}{\partial s_{k-1}} = W_s^T \cdot \text{diag}(f'(W_s s_{k-2} + W_x x_{k-1})) \]
也就是说,RNN的梯度是由多个线性变换与激活函数导数的连乘积组成。
对于常见的激活函数,例如tanh,其导数位于[0,1]之间,因此在多次连乘下极容易梯度消失。而当权重矩阵\(W_s\)过大时,又容易产生梯度爆炸问题。
解决方法:
梯度裁剪
将梯度范数超过阈值时进行缩放,可抑制梯度爆炸。
门控结构(LSTM/GRU)
LSTM和GRU都是通过门控加法机制实现信息传递。以LSTM为例:
\[ C_t = f_t \odot C_{t-1} + i_t \odot \tilde{C}_t \]
\[ \frac{\partial C_t}{\partial C_{t-1}} = f_t \]
\[ \frac{\partial L}{\partial C_{t-1}} = \frac{\partial L}{\partial C_t} \odot f_t \]
梯度只与门控值\(f_t\)相乘,而不涉及矩阵连乘。若\(f_t \approx 1\),梯度几乎可恒等传播;若\(f_t < 1\),梯度以可控方式衰减。
矩阵乘法会改变梯度的方向与长度,导致非线性扰动;而逐元素标量乘法不会改变方向,只调整幅度。门控\(f_t \in [0,1]\)还可以自适应地学习需要保留的梯度比例,从而在数值上保持稳定传播。